题目内容
1.关于x的方程x2-2mx+m2-1=0的两根x1、x2满足(2x1+x2)(x1+2x2)=6,求m的值.分析 根据根与系数的关系,得出x1+x2和x1•x2,再化简(2x1+x2)(x1+2x2)=6,求得m即可.
解答 解:∵x1、x2是关于x的方程x2-2mx+m2-1=0的两根,
∴x1+x2=2m,x1•x2=m2-1,
∵(2x1+x2)(x1+2x2)=6,
∴2x12+4x1x2+x1x2+2x22=6,
即2x12+5x1x2+2x22=6,
∴2(x1+x2)2+x1x2=6,
∴8m2+m2-7=0,
解得m=±$\frac{\sqrt{7}}{3}$,
当m=±$\frac{\sqrt{7}}{3}$时,方程有实数根,
∴m的值为±$\frac{\sqrt{7}}{3}$.
点评 本题主要考查了根与系数的关系的知识,解答本题的关键是掌握一元二次方程两根之和与两根之积与系数的关系,此题难度不大.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
11. 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )| A. | 64m2 | B. | 32m2 | C. | 128m2 | D. | 96m2 |
13.设“●”、“▲”、“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■,这三种物体按质量从大到小的顺序排列应为( )
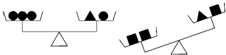

| A. | ●、▲、■ | B. | ■、▲、● | C. | ▲、■、● | D. | ■、●、▲ |
 如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.
如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.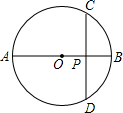 如图:⊙O的直径AB=10,CD是⊙O的弦,且CD⊥AB于P,已知BP:AP=1:4,则CD的长为( )
如图:⊙O的直径AB=10,CD是⊙O的弦,且CD⊥AB于P,已知BP:AP=1:4,则CD的长为( )