题目内容
3.如图1,?ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=$\sqrt{13}$,求AD的长;
(2)求证:EG=BG+FC;
(3)如图2,若AF=5$\sqrt{2}$,EF=2,点M是线段AG上的一个动点,连接ME,将△GME沿ME翻折得△G′ME,连接DG′,试求当DG′取得最小值时GM的长.
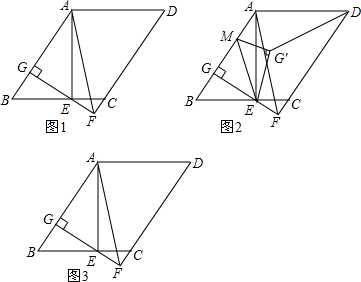
分析 (1)设AE=AD=BC=x,则BE=$\frac{2x}{3}$,CE=$\frac{1}{3}$x,根据勾股定理求出x,得到答案;
(2)作GH∥BC,交CD于点H,根据全等三角形的判定方法,判断出△AGE≌△GFH,即可证明EG=BG+FC;
(3)只有当E、G′、D在一条直线上时,DG′取得最小值,根据AF=5$\sqrt{2}$,EF=2,求出AG=GF=5,GE=G′E=3.已知AG,需要求GM,则需要先求AM.构造一个直角三角形:延长DA、G′M相较于点N,过点M作MP⊥AN,从而根据等腰直角三角形的性质和相似三角形的性质求出AM.
解答 (1)解:∵四边形ABCD为平行四边形,AE⊥BC,BE=2EC,
设AE=AD=BC=x,则BE=$\frac{2x}{3}$,CE=$\frac{1}{3}$x,
在Rt△ABE中,BE2+AE2=AB2,
即($\frac{2x}{3}$)2+x2=13,
解得x=±3,
即AD=3;
(2)证明:如图1,作GH∥BC,交CD于点H,
∵EG⊥AB,AB∥CD,
∴FG⊥CD,
∴∠GFH=90°,
∵AE⊥BC,GH∥BC,
∴AE⊥GH,
∴∠GAE+∠AGH=90°,
又∵∠FGH+∠AGH=90°,
∴∠GAE=∠FGH,
∵AE=AD,GH=AD,
∴AE=GH,
在△AGE和△GFH中,
$\left\{\begin{array}{l}{∠GAE=∠FGH}\\{∠AGE=∠GFH=90°}\\{AE=GH}\end{array}\right.$,
∴△AGE≌△GFH(AAS),
∴EG=FH=FC+CH,
又∵CH=BG,
∴EG=BG+FC.
(3)只有当E、G′、D在一条直线上时,DG′取得最小值.如图2.
由(2)得△AGE≌△GFH,
∴AG=GF,
在Rt△AGF中,
∵AF=5$\sqrt{2}$,
∴AG=GF=5,
又∵EF=2,
∴GE=GF-EF=5-2=3,
∵将△GME沿ME翻折得△G′ME,
∴G′E=GE=3,
在Rt△AGE中,
AE=$\sqrt{{AG}^{2}{+GE}^{2}}=\sqrt{{5}^{2}{+3}^{2}}=\sqrt{34}$,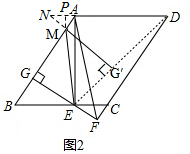
∵AE=AD,
∴在Rt△DAE中,ED=$\sqrt{2}$AE=2$\sqrt{17}$.
∴G′D=2$\sqrt{17}$-3.
延长DA、G′M相较于点N,过点M作MP⊥AN.
在Rt△NDG′中,
∵∠NDG′=45°,
∴NG′=DG′=2$\sqrt{17}$-3.
∴ND=$\sqrt{2}$DG′=2$\sqrt{34}$-3$\sqrt{2}$,
∴AN=ND-AD=2$\sqrt{34}$-3$\sqrt{2}$-$\sqrt{34}$=$\sqrt{34}$-3$\sqrt{2}$;
∵∠PAM+∠GAE=90°,∠GAE+∠AEG=90°,
∴∠PAM=∠AEG;
∴△PAM∽△GEA,
∴$\frac{PA}{PM}=\frac{GE}{AG}$=$\frac{3}{5}$.
在Rt△NDG′中,由∠NDG′=45°得∠N=45°,
∴NP=MP,
∴AP=$\frac{3}{8}$AN=$\frac{3}{8}$×($\sqrt{34}$-3$\sqrt{2}$),
∵由△PAM∽△GEA得$\frac{AM}{AE}=\frac{AP}{GE}$,即
∴AM=$\frac{\sqrt{34}}{3}$×$\frac{3}{8}$×($\sqrt{34}$-3$\sqrt{2}$)=$\frac{17-3\sqrt{17}}{4}$,.
∴GM=AG-AM=5-$\frac{17-3\sqrt{17}}{4}$=$\frac{3\sqrt{17}+3}{4}$.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合方法的应用;
(2)此题还考查了全等三角形的判定和性质的应用,以及相似三角形的判定和性质的应用,要熟练掌握;
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )| A. | 64m2 | B. | 32m2 | C. | 128m2 | D. | 96m2 |
| A. | ●、▲、■ | B. | ■、▲、● | C. | ▲、■、● | D. | ■、●、▲ |
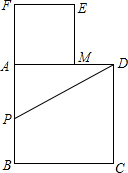 如图所示,以定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上(AM>MD).
如图所示,以定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上(AM>MD).
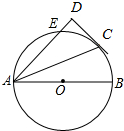 如图,AB是⊙O直径,Rt△ACD的直角边CD与⊙O相切,切点为C,直角边AD与⊙O相交于点E,∠BAC=22.5°,
如图,AB是⊙O直径,Rt△ACD的直角边CD与⊙O相切,切点为C,直角边AD与⊙O相交于点E,∠BAC=22.5°, 如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.
如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.