题目内容
10.当x是满足-2≤x≤2的整数时,求代数式($\frac{3}{x-2}$+$\frac{2}{x+2}$)÷$\frac{5{x}^{2}+2x}{{x}^{2}-4}$的值.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{3(x+2)+2(x-2)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x(5x+2)}$=$\frac{5x+2}{x(5x+2)}$=$\frac{1}{x}$,
∵x是满足-2≤x≤2的整数,
∴x可以取1,-1.
当x=1时,原式=1;
当x=-1时,原式=-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 两点之间的距离是两点间的线段 | |
| B. | 同一平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 与同一条直线垂直的两条直线也垂直 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
15.下列计算正确的是( )
| A. | (-3a)2=-9a2 | B. | $\frac{-a+b}{a+b}$=-1 | C. | 2a2-1=(2a+1)(2a-1) | D. | a3-4a3=-3a3 |
2.下列各数等于3的是( )
| A. | -$\sqrt{{3}^{2}}$ | B. | -$\sqrt{(-3)^{2}}$ | C. | (-$\sqrt{\frac{1}{3}}$)2 | D. | $\sqrt{(-\frac{1}{3})^{-2}}$ |
20.已知a<b,二次根式$\sqrt{-{a}^{3}b}$化简为( )
| A. | a$\sqrt{ab}$ | B. | a$\sqrt{-ab}$ | C. | -a$\sqrt{ab}$ | D. | -a$\sqrt{-ab}$ |

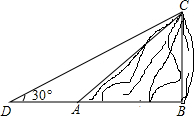 如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数). 已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.
已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.