题目内容
19. 已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.
已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.
分析 先把A(-1,4)代入y=$\frac{k}{x}$求出k得到反比例函数解析式为y=-$\frac{4}{x}$,再利用反比例函数解析式确定B(2,m),然后把A点和B点坐标代入y=ax+b得到关于a和b的方程组,于是解方程组求出a、b即可得到一次函数解析式.
解答 解:把A(-1,4)代入y=$\frac{k}{x}$得k=-1×4=-4,
所以反比例函数解析式为y=-$\frac{4}{x}$,
把B(2,m)代入y=-$\frac{4}{x}$得2m=-4,解得m=-2,
把A(-1,4),B(2,-2)代入y=ax+b得$\left\{\begin{array}{l}{-a+b=4}\\{2a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
所以一次函数解析式为y=-2x+2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
9.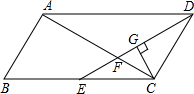 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 1cm | D. | $\frac{2}{3}\sqrt{3}$cm |
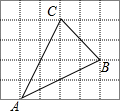 网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,
网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,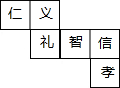 “仁义礼智信孝”是我们中华民族的传统美德,小明同学将这六个字分别写在一个正方体六个表面上,这个正方体的表面展开图如图所示,那么与“孝”所在面相对的面上的字是义.
“仁义礼智信孝”是我们中华民族的传统美德,小明同学将这六个字分别写在一个正方体六个表面上,这个正方体的表面展开图如图所示,那么与“孝”所在面相对的面上的字是义.