题目内容
 已知:
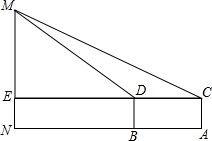
已知:(1)在测点A处安置侧倾器,测得此时M的仰角∠MCE=α.
(2)在测点A与物体MN之间的B处安置侧倾器(A,B与N在同一条直线上),测得此时M的仰角∠MDE=β.
(3)两处侧倾器的高度AC=BD=a,以及测点A和测点B之间的水平距离AB=b.
问:根据测量数据,你能求出物体MN的高度吗?说说你的理由.
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设ME=x,分别在Rt△MEC和Rt△MDE中表示出EC和ED的长度,然后根据EC-ED=CD=AB=b,求出x的值,继而可求得MN的高度.
解答:解:可以求得物体MN的高度;
根据题意可得:四边形ABCD和四边形ACEN为矩形,
则有EN=AC=BD=a,AB=CD=b,
设ME=x,
在Rt△MEC中,
∵∠MCE=α,
∴
=tan∠MCE=tanα,
∴CE=
,
在Rt△MDE中,
∵∠MDE=β,
∴
=tan∠MDE=tanβ,
∴DE=
,
∵EC-ED=CD=AB=b,
∴
-
=b,
∴x=b
,
∴MN=ME+EN=x+a=b
+a.
根据题意可得:四边形ABCD和四边形ACEN为矩形,
则有EN=AC=BD=a,AB=CD=b,
设ME=x,
在Rt△MEC中,
∵∠MCE=α,
∴
| ME |
| CE |
∴CE=
| x |
| tanα |
在Rt△MDE中,
∵∠MDE=β,
∴
| ME |
| DE |
∴DE=
| x |
| tanβ |
∵EC-ED=CD=AB=b,
∴
| x |
| tanα |
| x |
| tanβ |
∴x=b
| tanα•tanβ |
| tanβ-tanα |
∴MN=ME+EN=x+a=b
| tanα•tanβ |
| tanβ-tanα |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用公共边求解直角三角形,难度一般.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板,他购买的瓷砖形状不可以是( )
| A、正三角形 | B、长方形 |
| C、正八边形 | D、正六边形 |
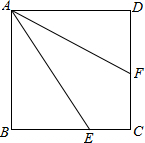 已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.
已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.