题目内容
18.设a、b、c满足$\left\{\begin{array}{l}{{a}^{2}-bc-8a+7=0}\\{{b}^{2}+{c}^{2}+bc-6a+6=0}\end{array}\right.$(1)求a的范围;
(2)对满足方程组(*)的任意a值,都有$\sqrt{a+3}$-a>m(m为常数),求m的范围.
分析 (1)①+②得a2+b2+c2=14a-13,进一步得到b2+c2=-a2+14a-13=-(a-7)2+36,根据非负数的性质即可求出a的取值范围;
(2)令t=$\sqrt{a+3}$,可得$\sqrt{a+3}$-a=-(t-$\frac{1}{2}$)2+$\frac{13}{4}$,把t的范围代入$\sqrt{a+3}$-a,可求m的范围.
解答 解:(1)$\left\{\begin{array}{l}{{a}^{2}-bc-8a+7=0①}\\{{b}^{2}+{c}^{2}+bc-6a+6=0②}\end{array}\right.$,
①+②得a2+b2+c2=14a-13,
b2+c2=-a2+14a-13=-(a-7)2+36,
∵b2+c2≥0,
∴-(a-7)2+36≥0,
∴(a-7)2≤36,
∴-6≤a-7≤6
∴1≤a≤13.
故a的范围为:1≤a≤13.
(2)令t=$\sqrt{a+3}$,
则t2=a+3,即a=t2-3,
则$\sqrt{a+3}$-a
=t-t2+3
=-(t-$\frac{1}{2}$)2+$\frac{13}{4}$
∵2≤t≤4,
∴$\sqrt{a+3}$-a的最小值是-(4-$\frac{1}{2}$)2+$\frac{13}{4}$=-9,
∴m<-9.
故m的范围是m<-9.
点评 本题考查的是高次方程、完全平方公式及最值问题,能把方程化为完全平方公式的形式是解答此题的关键.

练习册系列答案
相关题目
7. 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )
 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
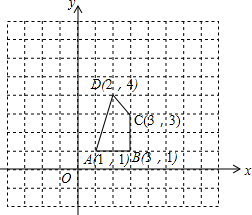 将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;
将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;
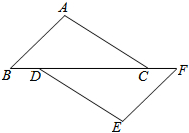 如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.
如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.