题目内容
6. 如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.
如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.
分析 连接PC,根据正方形的性质可得∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,然后求出四边形PMCN是矩形,根据矩形的对角线相等可得PC=MN,再利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,从而得解.
解答  解:连接PC,
解:连接PC,
∵四边形ABCD为正方形,
∴∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,
又∵PN⊥DC,PM⊥BC,
∴∠PMC=90°,∠PNC=90°,
∴四边形PMCN为矩形,
∴PC=MN,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBD}\\{PB=PB}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴AP=PC,
∴AP=MN.
点评 本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,作出辅助线,构造出全等三角形是解题的关键.

练习册系列答案
相关题目
17. 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
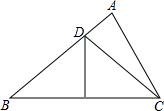 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.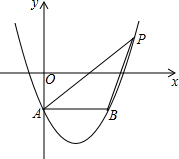 如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.
如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.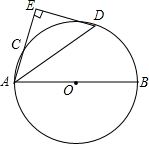 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.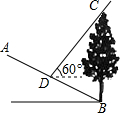 如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
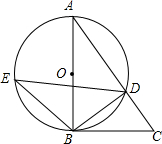 如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.