题目内容
16.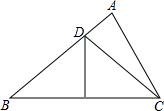 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
分析 根据线段垂直平分线的性质得到DB=DC,根据三角形内角和定理和等腰三角形的性质证明CA=CD=DB=8,根据三角形周长公式计算即可.
解答 解:∵BC的垂直平分线交AB于点D,
∴DB=DC,
∴∠DCB=∠B=40°,
∵∠A=80°,∠B=40°,
∴∠ACB=60°,
∴∠ACD=20°,
∴∠ADC=80°,
∴CA=CD=DB=8,
∴△ADC的周长=AD+AC+CD=19,
故答案为:19.
点评 本题考查的是线段垂直平分线的性质和三角形内角和定理以及等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在数1,0,-1,-100中,最小的数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -100 |
8.与-2的和为0的数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
5.为了参加社区“畅响G20”文艺演出,某校组建了46人的合唱队和30人的舞蹈队,现根据演出需要,从舞蹈队中抽调了部分同学参加合唱队,使合唱队的人数恰好是舞蹈队人数的3倍,设从舞蹈队中抽调了x人参加合唱队,可得正确的方程是( )
| A. | 3(46-x)=30+x | B. | 46+x=3(30-x) | C. | 46-3x=30+x | D. | 46-x=3(30-x) |
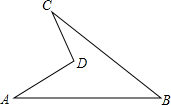 如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
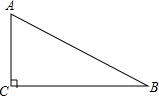 如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9.
如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9. 如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.
如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.