题目内容
16.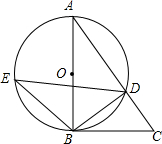 如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到ED连线经过点O的,试证明:△EDB≌△ABD.
分析 (1)欲证明BC是⊙O的切线,只需证得BC⊥AB即可;
(2)利用圆周角定理,全等三角形的判定定理AAS证得当点E运动到DE经过点O位置时,△EDB≌△ABD.
解答 证明:(1)∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ABD+∠BAD=90°.
又∵∠CBD=∠E,∠BAD=∠E,
∴∠ABD+∠CBD=90°,即∠ABC=90°.
∴BC⊥AB.
∴BC是⊙O的切线.
(2)当点E运动到DE经过点O位置时,△EDB≌△ABD.证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
在△EDB与△ABD中,
$\left\{\begin{array}{l}{∠EBD=∠ADB}\\{∠ABD=∠E}\\{BD=DB}\end{array}\right.$,
∴△EDB≌△ABD(AAS).
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了全等三角形的判定和性质以及圆周角定理定理的运用.

练习册系列答案
相关题目
11.据邵东县2016年政府工作报告显示,邵东县2015年财政总收入为18.94亿元,18.94亿元用科学记数法表示为( )元.
| A. | 18.948 | B. | 18.94×108 | C. | 1.894×109 | D. | 1.894×1010 |
8.一次外语口语考试中,某题(满分4分)的得分情况如下表:
求该题得分的平均数、众数和中位数.
| 得分/分 | 0 | 1 | 2 | 3 | 4 |
| 百分率 | 15% | 10% | 25% | 40% | 10% |
 如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.
如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.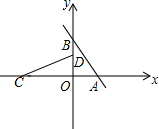 如图,直线y=-2x+4与x轴、y轴分别交于A、B两点,把△AOB绕着点O逆时针旋转90°得到△COD.
如图,直线y=-2x+4与x轴、y轴分别交于A、B两点,把△AOB绕着点O逆时针旋转90°得到△COD. 已知在平面直角坐标系中,已知A(3,4),B(3,-1),C(-3,-2),D(-2,3)
已知在平面直角坐标系中,已知A(3,4),B(3,-1),C(-3,-2),D(-2,3)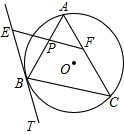 如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点.
如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点.