题目内容
14．
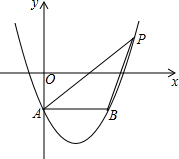如图，在平面直角坐标系中，抛物线y=x2-2x-1交y轴于点A，过点A作AB∥x轴交抛物线于点B，点P在抛物线上，连结PA、PB，若点P关于x轴的对称点恰好落在直线AB上，则△ABP的面积是2．
分析 求得C的坐标，进而求得B的坐标，根据点P关于x轴的对称点恰好落在直线AB上得出三角形的高，然后根据三角形面积公式即可求得．
解答 解：令x=0，则y=x2-2x-1=-1，
∴A（0，-1），
把y=-1代入y=x2-2x-1得-1=x2-2x-1，
解得x1=0，x2=2，
∴B（2，-1），
∴AB=2，
∵点P关于x轴的对称点恰好落在直线AB上，
∴△PAB边AB上的高为2，
∴S=$\frac{1}{2}$×2×2=2．
故答案为2．
点评 本题考查了二次函数图象上点的坐标特征，求得A、B的坐标以及三角形的高是解题的关键．
练习册系列答案
相关题目
4．在数1，0，-1，-100中，最小的数是（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | -100 |
5．为了参加社区“畅响G20”文艺演出，某校组建了46人的合唱队和30人的舞蹈队，现根据演出需要，从舞蹈队中抽调了部分同学参加合唱队，使合唱队的人数恰好是舞蹈队人数的3倍，设从舞蹈队中抽调了x人参加合唱队，可得正确的方程是（ ）
| A． | 3（46-x）=30+x | B． | 46+x=3（30-x） | C． | 46-3x=30+x | D． | 46-x=3（30-x） |
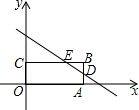如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴的正半轴上，点B在第一象限，直线y=$-\frac{2}{3}x+2$与边AB、BC分别交于点D、E，若点B的坐标为（m，1），则m的值可能是（ ）
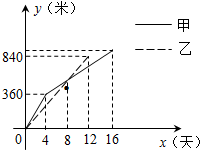某县在实施“村村通”工程中，决定在A、B两村之间修一条公路，甲、乙两个工程队分别从A、B两村同时开始相向修路，施工期间，甲队改变了一次修路速度，乙队因另有任务提前离开，余下的任务由甲队单独完成，直到公路修通，甲、乙两个工程队各自所修公路的长度y（米）与修路时间x（天）之间的函数图象如图所示．
如图，点P是正方形ABCD的对角线BD上的一点，PM⊥BC，PN⊥CD，垂足分别为点M，N．求证：AP=MN．