题目内容
20.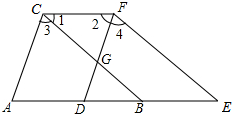 如图,已知B,D为AE上的两点,BC,DF交于点G,∠A=∠2,CF∥AE,∠3=∠4.求证:∠1=∠E.
如图,已知B,D为AE上的两点,BC,DF交于点G,∠A=∠2,CF∥AE,∠3=∠4.求证:∠1=∠E.
分析 根据平行线的性质和已知条件得到∠ACF=∠ADF,证得四边形ADFC是平行四边形,由平行四边形的性质得到AC∥DF,根据平行线的性质得到∠A=∠FDE,于是得到∠ABC=∠E,证得BC∥EF,求出∠E=∠ABC,然后根据平行线的性质即可得到结论.
解答 证明:∵∠A=∠2,CF∥AE,
∴∠A+∠ACF=∠2+∠ADF=180°,
∴∠ACF=∠ADF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠A=∠FDE,
∵∠3=∠4,
∴∠ABC=∠E,
∴BC∥EF,
∴∠E=∠ABC,
∵CF∥AE,
∴∠1=∠B,
∴∠1=∠E.
点评 本题考查了平行线的判定和性质,平行四边形的判定和性质,三角形的内角和,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
13.化简$\frac{5{x}^{3}y}{15{x}^{2}{y}^{2}}$的结果( )
| A. | $\frac{x}{10y}$ | B. | $\frac{{x}^{3}y}{10{x}^{2}{y}^{2}}$ | C. | $\frac{x}{3y}$ | D. | $\frac{{x}^{3}y}{3{x}^{2}{y}^{2}}$ |
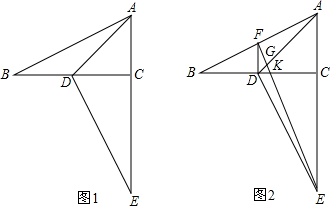
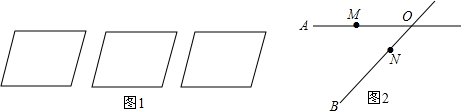
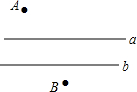 如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)
如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)