题目内容
8.(1)请用三种不同的方法把一个平行四边形分割成四个全等的图形(如图1).(2)如图2,某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)
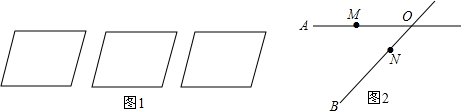
分析 (1)作图的时候要首先找到对角线的交点,只要过对角线的交点,任画一条直线即可.如图有:AE=BE=DF=CF,AM=CN;
(2)到两条公路的距离相等,在这两条公路的夹角的平分线上;到两所大学的距离相等,在这两所大学两个端点的连线的垂直平分线上,所画两条直线的交点即为所求的位置.
解答 解:(1)如图, ;
;
(2)如图2,则点P为所求. .
.
点评 本题考查的是作图-应用与设计作图,熟知平行四边形的性质与角平分线的性质是解答此题的关键.

练习册系列答案
相关题目
1.小磊解题时,将式子(-$\frac{1}{6}$)+(-7)+$\frac{5}{6}$+(-4)先变成[(-$\frac{1}{6}$)+$\frac{5}{6}$]+[(-7)+(-4)]再计算结果,则小磊运用了( )
| A. | 加法交换律 | B. | 加法交换律和加法结合律 | ||
| C. | 加法结合律 | D. | 无法判断 |
17.若x=0是关于x的方程(k-2)x2+3x+k2+2k-8=0的解,则k的值为( )
| A. | -4 | B. | 2 | C. | 2或-4 | D. | 不能确定 |
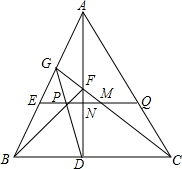 已知,如图,EQ∥BC,AD交BC于D,交EQ于N,CG交EQ于M,交AD于F,连接GD、BF交EQ于点P.求证:PM=MQ.
已知,如图,EQ∥BC,AD交BC于D,交EQ于N,CG交EQ于M,交AD于F,连接GD、BF交EQ于点P.求证:PM=MQ.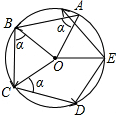 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
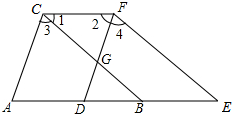 如图,已知B,D为AE上的两点,BC,DF交于点G,∠A=∠2,CF∥AE,∠3=∠4.求证:∠1=∠E.
如图,已知B,D为AE上的两点,BC,DF交于点G,∠A=∠2,CF∥AE,∠3=∠4.求证:∠1=∠E.