题目内容
8.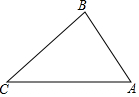 如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.
分析 作BD⊥AC,可得∠CBD=∠C=45°、∠ABD=30°,即可知BD=CD、AB=2AD,继而利用CD2+BD2=BC2可得BD=$\sqrt{3}$,利用BD2+AD2=AB2可得AD=1、AB=2.
解答 解:如图,过点B作BD⊥AC于点D,
∵∠C=45°,
∴∠CBD=∠C=45°,
∴BD=CD,
又∵∠ABC=75°,
∴∠ABD=30°,
∴AB=2AD,
在Rt△BCD中,由CD2+BD2=BC2可得2BD2=($\sqrt{6}$)2,
解得:BD=$\sqrt{3}$,
在Rt△ABD中,由BD2+AD2=AB2知($\sqrt{3}$)2+AD2=4AD2,
解得:AD=1,
则AB=2.
点评 本题主要考查勾股定理,熟练掌握特殊直角三角形各边之间的关系及勾股定理是解题的关键.

练习册系列答案
相关题目
19. 如图所示,下列说法中正确的是( )
如图所示,下列说法中正确的是( )
 如图所示,下列说法中正确的是( )
如图所示,下列说法中正确的是( )| A. | ∠2与∠3是同位角 | B. | ∠3与∠4是同旁内角 | ||
| C. | ∠1与∠2是内错角 | D. | ∠1与∠3是同旁内角 |
20.已知:关于x方程$\frac{x}{x+1}$+$\frac{x+1}{x}$=$\frac{4x+k}{{x}^{2}+x}$有且仅有一个实数根,则k的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或1 | C. | $\frac{1}{2}$或5或1 | D. | $\frac{1}{2}$或5或-2 |
16.若$\sqrt{{(2a+4)}^{2}}$=2a+4,则a的取值范围为( )
| A. | a≥2 | B. | a≤2 | C. | a≥-2 | D. | a≤-2 |
13.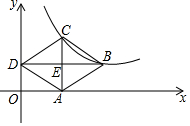 如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )
如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )
 如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )
如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )| A. | $y=\frac{2}{x}$ | B. | $y=\frac{3}{x}$ | C. | $y=\frac{{\sqrt{3}}}{x}$ | D. | $y=\frac{{2\sqrt{3}}}{x}$ |
 如图,在正方形ABCD中,点E是边CD上一点,点F是边BC的延长线上一点,连接BE、DF,且BE=DF.
如图,在正方形ABCD中,点E是边CD上一点,点F是边BC的延长线上一点,连接BE、DF,且BE=DF.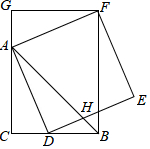 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论: