题目内容
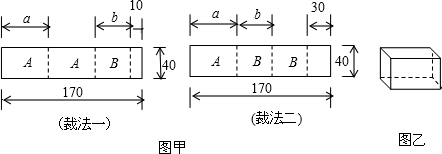
17.某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图所示,(单位:cm)(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将m张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒.
①两种裁法共产生A型板材2m+n张,B型板材m+2n张(用m、n的代数式表示);
②当30≤m≤40时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是24或27或30个.(在横线上直接写出所有可能答案,无需书写过程)
分析 (1)由图示利用板材的长列出关于a、b的二元一次方程组求解;
(2)①根据已知和图示计算出两种裁法共产生A型板材和B型板材的张数;
②根据竖式与横式礼品盒所需要的A、B两种型号板材的张数列出关于x、y的二元一次方程组,然后求解即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2a+b+10=170}\\{a+2b+30=170}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=60}\\{b=40}\end{array}\right.$;
(2)①由图示裁法一产生A型板材为:2×m=2m,裁法二产生A型板材为:1×n=n,
所以两种裁法共产生A型板材为2m+n(张),
由图示裁法一产生B型板材为:1×m=m,裁法二产生A型板材为,2×n=2n,
所以两种裁法共产生B型板材为(m+2n)张;
故答案为:2m+n;m+2n;24或27或30.
点评 本题考查的知识点是二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
相关题目
8.对于一个自然数n,如果能找到正整数x、y,使得n=x+y+xy,则称n为“好数”,例如:3=1+1+1×1,则3是一个“好数”,在8,9,10,11这四个数中,“好数”的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.根据某班40名同学一周的体育锻炼情况绘制了如下统计表,那么关于该班40名同学一周的体育锻炼时间的中位数是8.5小时.
| 时间(小时) | 7 | 8 | 9 | 10 |
| 人数(人) | 3 | 17 | 14 | 6 |
2.计算$\frac{x-1}{x}$+$\frac{1}{x}$=( )
| A. | 1 | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
6.已知a>b.若c是任意实数,则下列不等式中总是成立的是( )
| A. | a-c<b-c | B. | a+c>b+c | C. | ac<bc | D. | ac>bc |
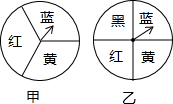 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.
如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.