题目内容
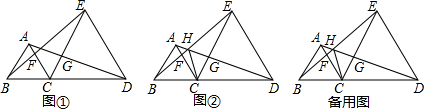
3.已知:在△ABC中,∠A:∠B:∠C=1:2:4,求证:$\frac{1}{BC}$=$\frac{1}{AC}$+$\frac{1}{AB}$.分析 延长AB至D,使BD=AC(此时,AD=AB+AC),又延长BC至E,使AE=AC,连接ED.设∠A=α,∠B=2α,∠C=4α,则∠A+∠B+∠C=7α=180°.得到BE=BD,△BDE是等腰三角形,相似三角形的性质即可得到结论.
解答 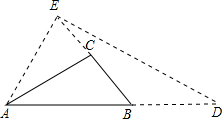 证明:延长AB至D,使BD=AC(此时,AD=AB+AC),又延长BC至E,使AE=AC,连接ED.
证明:延长AB至D,使BD=AC(此时,AD=AB+AC),又延长BC至E,使AE=AC,连接ED.
下面证明,△ADE∽△ABC.
设∠A=α,∠B=2α,∠C=4α,
则∠A+∠B+∠C=7α=180°.
由作图知,∠ACB是等腰三角形ACE的外角,
∴∠ACE=180°-4α=3α,
∴∠CAE=180°-3α-3α=7α-6α=α.
从而∠EAB=2α=∠EBA,AE=BE.
又由作图AE=AC,AE=BD,
∴BE=BD,△BDE是等腰三角形,
∴∠D=∠BED=α=∠CAB,
∴△ABC∽△DAE,
即$\frac{AD}{AE}$=$\frac{AB}{BC}$,即$\frac{AB+AC}{AC}$=$\frac{AB}{BC}$
∴$\frac{1}{BC}$=$\frac{1}{AC}$+$\frac{1}{AB}$.
点评 本题主要考查了相似三角形的判定及性质问题,能够利用其性质求解一些计算、证明问题.

练习册系列答案
相关题目
7.广东省某地冬季某天中午的气温是13℃,到午夜下降了14℃,那么午夜的气温是( )
| A. | 7℃ | B. | 1℃ | C. | -4℃ | D. | -1℃ |

 某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?
某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?