Question

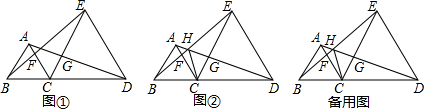
12．已知：△ABC和△CDE均为等边三角形，并且B、C、D三点共线．
（1）如图①，求证：△BCE≌△ACD；
（2）如图②，连结CH，求证：CH平分∠BHD；
（3）在图②中，试探究HD、HE、HC之间的数量关系，并证明．

Answer 1

分析 （1）根据等边三角形性质得出AC=BC，CE=CD，∠ACB=∠ECD=60°，求出∠BCE=∠ACD，根据SAS推出两三角形全等即可；
（2）作CM⊥BE、CN⊥AD，由△BCE≌△ACD，可知AD=BE，由全等三角形性质知CM=CN，据此得出CH平分∠BHD；
（3）在HD上截取DQ=EH，连接CQ，构造全等三角形，再根据全等三角形的性质，推理得出△CHQ为等边三角形，进而得到HQ=HC，最后根据HQ+DQ=HD，得到HC+HE=HD．

解答 （1）证明：∵△ABC和△CDE都是等边三角形，
∴BC=AC，CE=CD，∠BCA=∠ECD=60°，
∴∠BCA+∠ACE=∠ECD+∠ACE，即∠BCE=∠ACD，
在△BCE和△ACD中，
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$，
∴△BCE≌△ACD （SAS）；

（2）证明：如图②，作CM⊥BE，垂足为点M，作CN⊥AD，垂足为点N，
∵△BCE≌△ACD，
∴AD=BE，且S_△BCE=S_△ACD，
∵CM⊥AE，CN⊥BD，
∴$\frac{1}{2}$×BE×CM=$\frac{1}{2}$×AD×CN，
∴CM=CN，
又∵CM⊥AE，CN⊥BD，
∴点C在∠BHD的平分线上，即CH平分∠BHD；

（3）HC+HE=HD．
证明：如图，在HD上截取DQ=EH，连接CQ，
∵△BCE≌△ACD，
∴∠CDQ=∠CEH，
又∵CD=CE，
∴△CDQ≌△CEH（SAS），
∴∠DCQ=∠ECH，且CQ=CH，
又∵∠DCQ+∠ECQ=60°，
∴∠ECH+∠ECQ=60°，即∠HCQ=60°，
∴△CHQ为等边三角形，
∴HQ=HC，
又∵HQ+DQ=HD，
∴HC+HE=HD．

点评 本题考查的是等边三角形的判定与性质、全等三角形的判定与性质及角平分线的性质，结合等边三角形的性质，通过作辅助线构造全等三角形是正确解答本题的关键．解题时注意：全等三角形的对应边相等，对应角相等．