题目内容
2.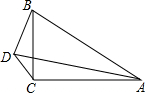 如图,△ABC中,∠ACB=90°,∠BAC=30°,D是△ABC外一点,∠BDC=120°,BD=2$\sqrt{3}$,CD=2,求S△ABD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,D是△ABC外一点,∠BDC=120°,BD=2$\sqrt{3}$,CD=2,求S△ABD.
分析 如图取AB中点M,连接CM、DM,在线段DM上截取DE=DB,作BF⊥DM于F,先证明DM=BD+DC,再求出DM、BF,求出△BDM的面积,根据S△ABD=2S△BDM即可解决问题.
解答 解:如图取AB中点M,连接CM、DM,在线段DM上截取DE=DB,作BF⊥DM于F.
在RT△ABC中,∵∠ACB=90°,∠BAC=30°,BM=AM,
∴∠ABC=60°,CM=BM=AM,
∴△BCM是等边三角形,
∴∠BMC=∠BCM=60°,
∵∠BDC=120°,
∴∠BDC+∠BMC=180°,
∴B、D、C、M四点共圆,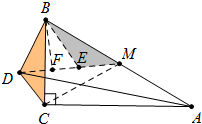
∴∠BDM=∠BCM=60°,∵DB=DE,
∴△BDE是等边三角形,
∴DB=DE,
∵∠DBE=∠CBM=60°,
∴∠DBC=∠EBM,
在△DBC和△EBM中,
$\left\{\begin{array}{l}{DB=BE}\\{∠DBC=∠EBM}\\{CB=BM}\end{array}\right.$,
∴△DBC≌△EBM,
∴CD=EM,
∴DM=DE+EM=DB+DC=2+2$\sqrt{3}$,
在RT△DBF中,∠BDF=60°,BD=2$\sqrt{3}$,
∴DF=$\frac{1}{2}$BD=$\sqrt{3}$,BF=$\sqrt{3}$DF=3,
∴S△BDM=$\frac{1}{2}$•DM•BF=$\frac{1}{2}$×(2+2$\sqrt{3}$)×3,
∵BM=AM,
∴S△ABD=2S△BDM=6+6$\sqrt{3}$.
点评 本题考查全等三角形的判定和性质、直角三角形斜边中线定理、等边三角形的判定和性质、特殊角的三角函数等知识,解题的关键是添加辅助线构造全等三角形,本题有一定难度,用到四点共圆,记住图中DM=BD+DC这个基本结论,属于中考常考题型.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 不变 | B. | 扩大3倍 | C. | 扩大9倍 | D. | 扩大6倍 |
 如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC,若BD=1,则AD的长为$\sqrt{3}$.
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC,若BD=1,则AD的长为$\sqrt{3}$. 已知:在△ABC中,AB=AC,∠A=60°,求:∠B、∠C的度数,△ABC是什么三角形?
已知:在△ABC中,AB=AC,∠A=60°,求:∠B、∠C的度数,△ABC是什么三角形? 直线l1∥l2,一块含45°角的直角三角尺如图所示放置,∠1=85°,则∠2=130°.
直线l1∥l2,一块含45°角的直角三角尺如图所示放置,∠1=85°,则∠2=130°.