题目内容
12.计算(1)$\sqrt{2}$+3$\sqrt{2}$-5$\sqrt{2}$
(2)$\root{3}{8}$+$\sqrt{(-2)^{2}}$-$\sqrt{\frac{1}{4}}$
(3)$\sqrt{81}$+$\root{3}{-27}$+$\sqrt{(-\frac{2}{3})^{2}}$
(4)$\sqrt{2}$-1+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|
(5)π+$\sqrt{3}$-$\frac{2}{3}$.(精确到0.01)
分析 (1)直接合并同类二次根式进而得出答案;
(2)利用立方根以及算术平方根的定义化简求出答案;
(3)利用立方根以及算术平方根的定义化简求出答案;
(4)直接利用去绝对值,再合并同类二次根式进而得出答案;
(5)首先得出各数的近似值进而求出答案.
解答 解:(1)$\sqrt{2}$+3$\sqrt{2}$-5$\sqrt{2}$=-$\sqrt{2}$;
(2)$\root{3}{8}$+$\sqrt{(-2)^{2}}$-$\sqrt{\frac{1}{4}}$=2+2-$\frac{1}{2}$=$\frac{7}{2}$;
(3)$\sqrt{81}$+$\root{3}{-27}$+$\sqrt{(-\frac{2}{3})^{2}}$=9-3+$\frac{2}{3}$=6$\frac{2}{3}$;
(4)$\sqrt{2}$-1+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=1;
(5)π+$\sqrt{3}$-$\frac{2}{3}$(精确到0.01)
=3.1415-1.732-$\frac{2}{3}$
≈0.74.
点评 此题主要考查了实数运算,正确化简各数是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
7.在-1.732,$\sqrt{2}$,π,3.$\stackrel{••}{14}$,2+$\sqrt{3}$,3.212212221…,6.5这些数中,无理数的个数为( )
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
17.已知方程:
①2x+$\frac{1}{y}$=3;②5xy-1=0;③x2+y=2;④3x-y+z=0;⑤4x=$\frac{y-2}{4}$;⑥2x-y=3;⑦x+3=5
其中是二元一次方程的有( )个.
①2x+$\frac{1}{y}$=3;②5xy-1=0;③x2+y=2;④3x-y+z=0;⑤4x=$\frac{y-2}{4}$;⑥2x-y=3;⑦x+3=5
其中是二元一次方程的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.下列图形中,不一定是轴对称图形的是( )
| A. | 直角三角形 | B. | 线段 | C. | 钝角 | D. | 等腰三角形 |
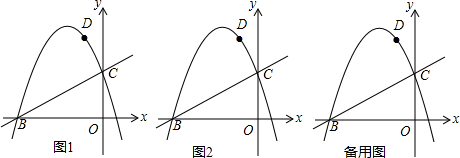
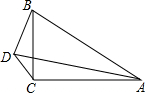 如图,△ABC中,∠ACB=90°,∠BAC=30°,D是△ABC外一点,∠BDC=120°,BD=2$\sqrt{3}$,CD=2,求S△ABD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,D是△ABC外一点,∠BDC=120°,BD=2$\sqrt{3}$,CD=2,求S△ABD.