题目内容
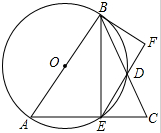 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.(1)判断直线BF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4,BD=3,求CE的长.
考点:切线的判定
专题:计算题
分析:(1)连结AD,如图,根据圆周角定理,由AB为直径得到∠1+∠ABD=90°,∠1=∠BED,而∠DBF=∠BED,所以∠DBF=∠1,则∠DBF+∠ABD=90°,即∠ABF=90°,于是根据切线的判定定理即可得到BF为⊙O的切线;
(2)根据等腰三角形的性质由AC=AB=8,∠ADB=90°,得到BD=CD=3,在Rt△ABD中利用勾股定理计算出AD=
,再由AB为直径得到∠AEB=90°,则可利用面积法计算出BE=
=
,然后在Rt△BEC中利用勾股定理可计算出CE.
(2)根据等腰三角形的性质由AC=AB=8,∠ADB=90°,得到BD=CD=3,在Rt△ABD中利用勾股定理计算出AD=
| 55 |
| ||
| 8 |
3
| ||
| 4 |
解答:解:(1)BF与⊙O相切.理由如下:
连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴∠1+∠ABD=90°,
∵∠DBF=∠BED,∠1=∠BED,
∴∠DBF=∠1,
∴∠DBF+∠ABD=90°,即∠ABF=90°,
∴AB⊥BF,
∴BF为⊙O的切线;
(2)∵AC=AB=8,
而∠ADB=90°,
∴BD=CD=3,
在Rt△ABD中,∵BD=3,AB=8,
∴AD=
=
,
∵AB为直径,
∴∠AEB=90°,
∴
AC•BE=
AD•BC,
∴BE=
=
,
在Rt△BEC中,∵BE=
,BC=6,
∴CE=
=
.

连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴∠1+∠ABD=90°,
∵∠DBF=∠BED,∠1=∠BED,
∴∠DBF=∠1,
∴∠DBF+∠ABD=90°,即∠ABF=90°,
∴AB⊥BF,
∴BF为⊙O的切线;
(2)∵AC=AB=8,
而∠ADB=90°,
∴BD=CD=3,
在Rt△ABD中,∵BD=3,AB=8,
∴AD=
| AB2-BD2 |
| 55 |
∵AB为直径,
∴∠AEB=90°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| ||
| 8 |
3
| ||
| 4 |
在Rt△BEC中,∵BE=
3
| ||
| 4 |
∴CE=
| BC2-BE2 |
| 9 |
| 4 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理.

练习册系列答案
相关题目
 如图所示,⊙O的半径为R,AB、CD是⊙O的任意两条弦,且AB垂直CD于M,求:AB2+(CM-DM)2.
如图所示,⊙O的半径为R,AB、CD是⊙O的任意两条弦,且AB垂直CD于M,求:AB2+(CM-DM)2. 如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=
如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=