题目内容
已知在Rt△ABC中,∠C=90°,
(1)若a=36,∠B=30°.求:∠A的度数和边b、c的长;
(2)若a=6
,b=6
.求:∠A、∠B的度数和边c的长.
(1)若a=36,∠B=30°.求:∠A的度数和边b、c的长;
(2)若a=6
| 2 |
| 6 |
考点:解直角三角形
专题:
分析:(1)直角三角形的两个锐角互余,并且Rt△ABC中,∠C=90°则∠A=90-∠B=60°,°解直角三角形就是求直角三角形中出直角以外的两锐角,三边中的未知的元素.
(2)利用tanA=
,再利用三角函数求∠A的度数,再利用直角三角形两锐角互余求出∠B的度数,进一步根据三角函数求出边c的长.
(2)利用tanA=
| a |
| b |
解答: 解:(1)如图,在Rt△ABC中,∵∠B=30°,a=36,
解:(1)如图,在Rt△ABC中,∵∠B=30°,a=36,
∴∠A=90-∠B=60°,
=cosB,即c=
=
=24
,
∴b=
c=
×24
=12
(30°角所对的直角边是斜边的一半);
 (2)如图,在Rt△ABC中,∵a=6
(2)如图,在Rt△ABC中,∵a=6
,b=6
,
∴tanA=
=
,
∴∠A=30°,
∴∠B=60°,
∴c=2a=12
.
 解:(1)如图,在Rt△ABC中,∵∠B=30°,a=36,
解:(1)如图,在Rt△ABC中,∵∠B=30°,a=36,∴∠A=90-∠B=60°,
| a |
| c |
| a |
| cosB |
| 36 | ||||
|
| 3 |
∴b=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
 (2)如图,在Rt△ABC中,∵a=6
(2)如图,在Rt△ABC中,∵a=6| 2 |
| 6 |
∴tanA=
| a |
| b |
| ||
| 3 |
∴∠A=30°,
∴∠B=60°,
∴c=2a=12
| 2 |
点评:此题主要考查了解直角三角形的条件,已知三角形的一边与一个锐角,就可以求出另一个锐角与三角形的另外两边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四边形ABCD的四个顶点都在⊙O上,AC⊥BD于E,OF⊥AB于F,求证:2OF=CD.
如图,四边形ABCD的四个顶点都在⊙O上,AC⊥BD于E,OF⊥AB于F,求证:2OF=CD. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是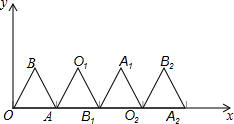 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为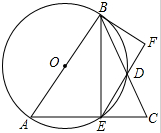 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.