题目内容
 如图所示,⊙O的半径为R,AB、CD是⊙O的任意两条弦,且AB垂直CD于M,求:AB2+(CM-DM)2.
如图所示,⊙O的半径为R,AB、CD是⊙O的任意两条弦,且AB垂直CD于M,求:AB2+(CM-DM)2.考点:垂径定理,勾股定理
专题:
分析:过点O作OE⊥AB,OF⊥CD,连接OB,根据垂径定理和勾股定理即可得出AB2+(CM-DM)2=4R2.
解答: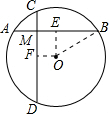 解:过点O作OE⊥AB,OF⊥CD,连接OB,
解:过点O作OE⊥AB,OF⊥CD,连接OB,
∴AB=2AE=2BE,CD=2CE=2DE,
∴在Rt△OBE中,OB2=OE2+BE2,
∵OB=R,
∴OE2+BE2=R2,
∴AB2+(CM-DM)2=AB2+(DM-CM)2
=AB2+(DF+MF-CM)2
=AB2+(CF+MF-CM)2
=AB2+(2MF)2
=(2BE)2+4MF2
=4BE2+4MF2
=4(BE2+OE2)
=4OB2
=4R2.
 解:过点O作OE⊥AB,OF⊥CD,连接OB,
解:过点O作OE⊥AB,OF⊥CD,连接OB,∴AB=2AE=2BE,CD=2CE=2DE,
∴在Rt△OBE中,OB2=OE2+BE2,
∵OB=R,
∴OE2+BE2=R2,
∴AB2+(CM-DM)2=AB2+(DM-CM)2
=AB2+(DF+MF-CM)2
=AB2+(CF+MF-CM)2
=AB2+(2MF)2
=(2BE)2+4MF2
=4BE2+4MF2
=4(BE2+OE2)
=4OB2
=4R2.
点评:本题考查了垂径定理以及勾股定理,常见的辅助线是过圆心作弦的垂线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成10个三角形,则n的值是( )
| A、11 | B、12 | C、13 | D、14 |
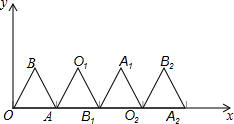 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为 (1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);
(1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);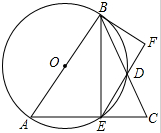 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.