题目内容
如图，点A、O、B在一条直线上，∠AOC=140°，OD是∠BOC的平分线，则∠COD=考点：角平分线的定义
专题：
分析：先根据邻补角的定义求出∠BOC的度数，然后根据角平分线的定义即可求出∠COD度数．
解答：解：∵∠AOC与∠BOC是邻补角，
∴∠AOC+∠BOC=180°，
∵∠AOC=140°，
∴∠BOC=180°-140°=40°，
∵OD平分∠BOC，
∴∠COD=
∠COB=20°．
故答案为：20．
∴∠AOC+∠BOC=180°，
∵∠AOC=140°，
∴∠BOC=180°-140°=40°，
∵OD平分∠BOC，
∴∠COD=
| 1 |
| 2 |
故答案为：20．
点评：此题考查了角平分线的定义及邻补角的定义，解题的关键是根据邻补角的定义求出∠BOC的度数．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①c＜0，②b＞0，③4a+2b+c＞0，④（a+c）2＜b2，⑤b+2a=0；⑥△＜0，其中正确的是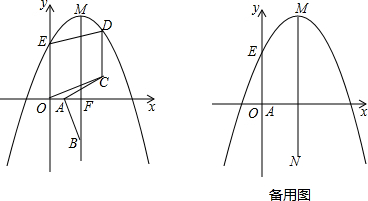
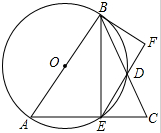如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，连接BE、ED，过点B的直线交ED的延长线于F，且∠DBF=∠BED．
如图，图中有
请从以下两个小题中任选一个作答，若多选，则按所选的第一题计分．下列各组二次根式中，是同类二次根式的是（ ）
A、
| ||||||
B、3
| ||||||
C、
| ||||||
D、
|