题目内容
∵
=
×(1-
),
=
(
-
),
=
(
-
)…
∴
+
+
=
×(1-
)+
×(
-
)+
×(
-
)=…
(1)按此规律,在算式
+
+
+…中,第6项为 ,前6项和为多少?请写出计算前6项求和过程;
(2)按此规律,在算式
+
+
+…中,第n项为 ,前n项和为多少?请写出计算前n项求和过程;
(3)按此规律,前n项和可以是
吗?若是,这是前多少项的和?请写出计算过程.
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
∴
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
(1)按此规律,在算式
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
(2)按此规律,在算式
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
(3)按此规律,前n项和可以是
| 100 |
| 201 |
考点:规律型:数字的变化类
专题:
分析:由题意可知:分母是两个相邻奇数的乘积,分子是1的分数可以拆成分子是1,分母是这两个奇数的分数的差,由此得出规律:
=
-
;
(1)(2)利用以上规律得出答案,进一步拆项抵消计算即可;
(3)利用(2)的计算结果判定即可.
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(1)(2)利用以上规律得出答案,进一步拆项抵消计算即可;
(3)利用(2)的计算结果判定即可.
解答:解:(1)第6项为
,
前6项和为
+
+
+…+
=
×(1-
+
-
+
-
+…+
-
)
=
×(1-
)
=
×
=
;
(2)第n项为
,
前n项和为
+
+
+…+
═
×(1-
+
-
+
-
+…+
-
)
=
×(1-
)
=
×
=
;
(3)∵
=
,
∴n=100.
∴这是前100项的和.
+
+
+…+
=
×(1-
+
-
+
-
+…+
-
)
=
×(1-
)
=
×
=
.
| 1 |
| 11×13 |
前6项和为
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 11×13 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 11 |
| 1 |
| 13 |
=
| 1 |
| 2 |
| 1 |
| 13 |
=
| 1 |
| 2 |
| 10 |
| 13 |
=
| 5 |
| 13 |
(2)第n项为
| 1 |
| (2n-1)(2n+1) |
前n项和为
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| (2n-1)(2n+1) |
═
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 2n |
| 2n+1 |
=
| n |
| 2n+1 |
(3)∵
| n |
| 2n+1 |
| 100 |
| 201 |
∴n=100.
∴这是前100项的和.
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 199×201 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 199 |
| 1 |
| 201 |
=
| 1 |
| 2 |
| 1 |
| 201 |
=
| 1 |
| 2 |
| 200 |
| 201 |
=
| 100 |
| 201 |
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成10个三角形,则n的值是( )
| A、11 | B、12 | C、13 | D、14 |
在实数
,
,
,π,-2,
,
,
,
,0中,无理数的个数是( )
| 3 | 9 |
| 1 |
| 3 |
| 7 |
| 2 |
|
| 3 | 8 |
|
| A、4 | B、5 | C、6 | D、7 |
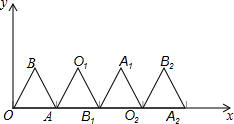 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为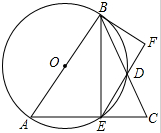 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED. 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.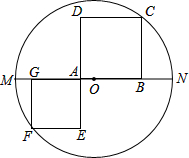 如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为
如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为 如图,A、B是4×5网格中的格点,网格中的每个小正方形的边长都是1,请在图中格点上清晰标出一点C,使以A、B、C为顶点的三角形是等腰三角形,且三边长均为无理数.
如图,A、B是4×5网格中的格点,网格中的每个小正方形的边长都是1,请在图中格点上清晰标出一点C,使以A、B、C为顶点的三角形是等腰三角形,且三边长均为无理数.