题目内容
3.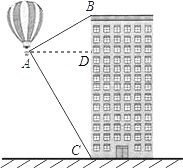 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高160$\sqrt{3}$m(结果保留根号).
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高160$\sqrt{3}$m(结果保留根号).
分析 过A作AD⊥BC,垂足为D,在直角△ABD与直角△ACD中,根据三角函数即可求得BD和CD,即可求解.
解答 解:过A作AD⊥BC,垂足为D,如图所示: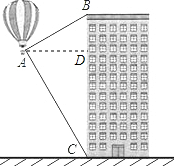
在Rt△ABD中,
∵∠BAD=30°,AD=120m,
∴BD=AD•tan30°=120×$\frac{\sqrt{3}}{3}$=40$\sqrt{3}$m,
在Rt△ACD中,
∵∠CAD=60°,AD=120m,
∴CD=AD•tan60°=120×$\sqrt{3}$=120$\sqrt{3}$m,
BC=BD+CD=160$\sqrt{3}$m.
即这栋楼高为160$\sqrt{3}$m.
故答案为:160$\sqrt{3}$.
点评 本题主要考查了仰角与俯角的计算,一般三角形的计算,常用的方法是利用作高线转化为直角三角形的计算.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
14.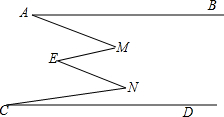 如图,AB∥CD,则下列结论正确的是( )
如图,AB∥CD,则下列结论正确的是( )
 如图,AB∥CD,则下列结论正确的是( )
如图,AB∥CD,则下列结论正确的是( )| A. | ∠M+∠N=∠A+∠E+∠C | B. | ∠M+∠N<∠A+∠E+∠C | C. | ∠M=∠N | D. | ∠E=∠A+∠C |
 如图,在平面直角坐标系中,顶点为(2,-1)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,3),连接AB.
如图,在平面直角坐标系中,顶点为(2,-1)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,3),连接AB. 如图所示,A、B之间是一座山,一条铁路要通过A、B两地,在A地测得铁路走向是北偏东48°25′,则在B地测得A地在南偏西多少度?如果A、B两地同时开工,那么在B地按∠β施工,∠β为多少度才能使铁路在山腹中准确接通?
如图所示,A、B之间是一座山,一条铁路要通过A、B两地,在A地测得铁路走向是北偏东48°25′,则在B地测得A地在南偏西多少度?如果A、B两地同时开工,那么在B地按∠β施工,∠β为多少度才能使铁路在山腹中准确接通?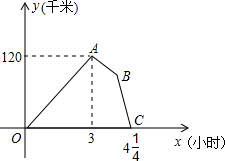 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示. 如图,AB∥DC,AD∥BC,E为BC延长线上一点,连结AE与CD相交于点F,若∠CFE=∠E. 试说明AE平分∠BAD.
如图,AB∥DC,AD∥BC,E为BC延长线上一点,连结AE与CD相交于点F,若∠CFE=∠E. 试说明AE平分∠BAD.