题目内容
13.当x=$\sqrt{3}$,y=$\sqrt{2}$时,求代数式$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$+[$\frac{\sqrt{x}}{x+\sqrt{xy}}-\frac{\sqrt{y}}{y-\sqrt{xy}}$]$÷\frac{1}{\sqrt{y}}$的值.分析 先计算括号,分子分母因式分解约分后去括号,再通分化简,最后代入即可.
解答 解:原式=$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$+[$\frac{1}{\sqrt{x}+\sqrt{y}}$-$\frac{1}{\sqrt{y}-\sqrt{x}}$]•$\sqrt{y}$
=$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$+$\frac{\sqrt{y}}{\sqrt{x}+\sqrt{y}}$+$\frac{\sqrt{y}}{\sqrt{x}-\sqrt{y}}$
=$\frac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}$+$\frac{\sqrt{y}}{\sqrt{x}-\sqrt{y}}$
=$\frac{\sqrt{x}(\sqrt{x}-\sqrt{y})+\sqrt{y}(\sqrt{x}+\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y)}}$
=$\frac{x+y}{x-y}$,
∵x=$\sqrt{3}$,y=$\sqrt{2}$,
∴原式=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$.
点评 本题考查二次根式的化简求值、熟练掌握二次根式的混合运算法则是解题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.方程x2+4x-4=0的左边配成完全平方后所得的方程为( )
| A. | (x+2)2=8 | B. | (x-2)2=8 | C. | (x+2)2=4 | D. | (x-2)2=4 |
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(a,6),B(3,a+1)两点
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(a,6),B(3,a+1)两点 如图,矩形纸片ABCD,用如下方法折叠该纸片:
如图,矩形纸片ABCD,用如下方法折叠该纸片: 如图,若∠B=50°,则∠∠ADE=50°时,DE∥BC,理由是同位角相等,两直线平行.
如图,若∠B=50°,则∠∠ADE=50°时,DE∥BC,理由是同位角相等,两直线平行. 如图,当∠1=∠3时,AB∥CD.
如图,当∠1=∠3时,AB∥CD.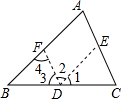 已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)
已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)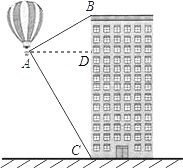 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高160$\sqrt{3}$m(结果保留根号).
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高160$\sqrt{3}$m(结果保留根号).