题目内容
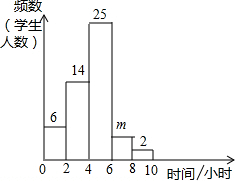小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了如图所示的频率分布直方图．若从参加课外活动时间在6～10小时的5名学生中随机选取2人，则其中至少有1人课外活动时间在8～10小时的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：列表法与树状图法,频数（率）分布直方图
专题：计算题
分析：根据小明所在班级人数为50人，由统计图求出m的值，找出所有等可能的情况数及至少有1人课外活动时间在8～10小时的情况数，即可求出所求的概率．
解答：解：由题意得：50-（6+14+25+2）=50-47=3（人），
设参加课外活动时间为6～8小时的3人为A，A，A；参加课外活动时间8～10小时的2人为B，B，
所有等可能的情况有：（A，A）；（A，A）；（A，B）；（A，B）；（A，A）；（A，A）；（A，B）；（A，B）；（A，A）；（A，A）；（A，B）；（A，B）；（B，A）；（B，A）；（B，A）；（B，B）；（B，A）；（B，A）；（B，A）；（B，B），共20种，
其中至少有1人课外活动时间在8～10小时的情况有14种，
则P=
=
，
故选A
设参加课外活动时间为6～8小时的3人为A，A，A；参加课外活动时间8～10小时的2人为B，B，
所有等可能的情况有：（A，A）；（A，A）；（A，B）；（A，B）；（A，A）；（A，A）；（A，B）；（A，B）；（A，A）；（A，A）；（A，B）；（A，B）；（B，A）；（B，A）；（B，A）；（B，B）；（B，A）；（B，A）；（B，A）；（B，B），共20种，
其中至少有1人课外活动时间在8～10小时的情况有14种，
则P=
| 14 |
| 20 |
| 7 |
| 10 |
故选A
点评：此题考查了列表法与树状图法，以及频数（率）分布直方图，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知△ABC为等腰直角三角形，∠BAC=90°，BE是∠ABC的平分线，DE⊥BC，垂足为D．
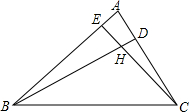如图，BD，CE分别是△ABC的两条高、它们相交于点H，那么下列式子中正确的有（ ）个．（1）∠DHC=∠A；（2）∠EBH+∠A=90°；（3）∠ACE=∠ABD；（4）∠ECB=∠ABC．
| A、1 | B、2 | C、3 | D、4 |
下列图形中，表示立体图形的个数是（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，点A，B，C，D为⊙O上的四个点，AC交BD于点E，∠DAC=∠BDC，CE=4，CD=6，则AE的长为（ ）下列说法正确的是（ ）
A、某种彩票中奖的概率是
| ||
| B、为了了解某批灯泡的使用寿命可以用普查的方式 | ||
| C、“在同一年出生的367名学生中，至少有两人的生日是同一天”是必然事件 | ||
| D、在一个装有白球和绿球的袋中摸球，摸出白球和摸出绿球是等可能事件 |
如图，直线AB、CD被直线EF所截，AB∥CD，∠1=105°，则∠2等于（ ）| A、65° | B、70° |
| C、75° | D、80° |