题目内容
 如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.(1)写出图中所有的等腰三角形,不需证明;
(2)请你判断AD与BE是否垂直,并说明理由;
(3)如果BC=12,求AB+AE的长.
考点:全等三角形的判定与性质,角平分线的性质,等腰三角形的判定与性质
专题:
分析:(1)易证BE是AD的垂直平分线,根据线段的垂直平分线以及等腰直角三角形的定义即可作出判断;
(2)证明△ABE≌△DBE,则AE=DE,AB=BD,即可得到BE是线段AD的中垂线;
(3)根据AE=ED,以及△EDC是等腰直角三角形,即可得到AB+AE=BC,从而求解.
(2)证明△ABE≌△DBE,则AE=DE,AB=BD,即可得到BE是线段AD的中垂线;
(3)根据AE=ED,以及△EDC是等腰直角三角形,即可得到AB+AE=BC,从而求解.
解答:解:(1)△ABC、△ABD、△AED、△EDC;
(2)AD⊥BE.
理由:在△ABE和△DBE中,
,
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).

(2)AD⊥BE.
理由:在△ABE和△DBE中,
|
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).
点评:本题考查了线段的垂直平分线的判定与性质,以及全等三角形的判定与性质,理解线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两端的距离相等,是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
在Rt△ABC中,∠A=Rt∠,AC=6,BC=8,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某种商品的进价为1600元,新年期间,商场为了促销,对该商品按标价的8折出售,仍可获利160元,则该商品的标价应为( )
| A、2400元 |
| B、2200元 |
| C、2000元 |
| D、1800元 |
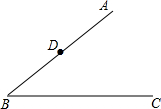 如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:
如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题: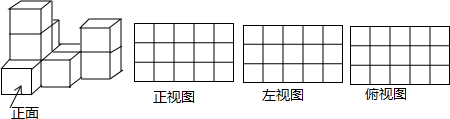
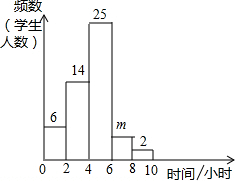 小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了如图所示的频率分布直方图.若从参加课外活动时间在6~10小时的5名学生中随机选取2人,则其中至少有1人课外活动时间在8~10小时的概率为( )
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了如图所示的频率分布直方图.若从参加课外活动时间在6~10小时的5名学生中随机选取2人,则其中至少有1人课外活动时间在8~10小时的概率为( )