题目内容
5．
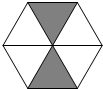如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成，一只小鸟在广场上随机停留，刚好落在黑色三角形区域的概率为$\frac{1}{3}$．
分析 刚好落在黑色三角形上的概率就是黑色三角形面积与总面积的比值，从而得出答案．
解答 解：∵黑色三角形的面积占总面积的$\frac{2}{6}$=$\frac{1}{3}$，
∴刚好落在黑色三角形区域的概率为$\frac{1}{3}$；
故答案为：$\frac{1}{3}$．
点评 本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
练习册系列答案
相关题目
15．
正方形网格中，∠AOB如图放置，则∠AOB的正弦值为（ ）
正方形网格中，∠AOB如图放置，则∠AOB的正弦值为（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{2}$ | D． | 2 |
17．若x2+4x-4=0，则3（x-2）2-6（x+1）（x-1）的值为（ ）
| A． | -6 | B． | 6 | C． | 18 | D． | 30 |
4．一个两位数的十位数字与个位数字的和是8，把这个两位数加上18，结果恰好成为数字对调后组成的两位数，求这个两位数，设个位数字为x，十位数字为y，所列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=8}\\{10（x+y）+18=yx}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |