题目内容
1. 在Rt△ABC中,∠C=90°,tanB=$\frac{3}{4}$,∠ADC=45°,DC=6,求sin∠BAD.
在Rt△ABC中,∠C=90°,tanB=$\frac{3}{4}$,∠ADC=45°,DC=6,求sin∠BAD.
分析 作DE⊥AB于E,如图,先判断△ACD为等腰直角三角形得到AC=CD=6,AD=$\sqrt{2}$CD=6$\sqrt{2}$,再在Rt△ABC中利用∠B的正切可求出BC=8,则BD=BC-CD=2,接着在Rt△BDE中,由于tanB=$\frac{DE}{BE}$=$\frac{3}{4}$,则可设DE=3x,BE=4x,所以BD=5x=2,解得x=$\frac{2}{5}$,则DE=3x=$\frac{6}{5}$,然后在Rt△ADE中利用正弦的定义求解.
解答 解:作DE⊥AB于E,如图,
∵∠C=90°,∠ADC=45°,
∴△ACD为等腰直角三角形,
∴AC=CD=6,AD=$\sqrt{2}$CD=6$\sqrt{2}$,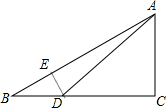
在Rt△ABC中,∵tanB=$\frac{AC}{BC}$=$\frac{3}{4}$,
∴BC=8,
∴BD=BC-CD=2,
在Rt△BDE中,tanB=$\frac{DE}{BE}$=$\frac{3}{4}$,
设DE=3x,BE=4x,则BD=5x,
∴5x=2,解得x=$\frac{2}{5}$,
∴DE=3x=$\frac{6}{5}$,
在Rt△ADE中,sin∠EAD=$\frac{DE}{AD}$=$\frac{\frac{6}{5}}{6\sqrt{2}}$=$\frac{{\sqrt{2}}}{10}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是构建一个直角三角形,使∠BAD为其一个内角.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.粗心的小红在计算n边形的内角和时,少加了一个内角,求得的内角和是2040°,则这个多边形的边数n和这个内角分别是( )
| A. | 11和60° | B. | 11和120° | C. | 12和60° | D. | 14和120° |
 某物流公司的甲、乙两辆货车分别从相距600千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶3小时时甲车先到达配货站C地,此时两车相距60千米,甲车在C地用1小时配货,然后按原速度开
某物流公司的甲、乙两辆货车分别从相距600千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶3小时时甲车先到达配货站C地,此时两车相距60千米,甲车在C地用1小时配货,然后按原速度开 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A(-2,0),C(4,0)两点,和y轴相交于点B,连接AB、BC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A(-2,0),C(4,0)两点,和y轴相交于点B,连接AB、BC. 如图,已知Rt△ABC中,斜边BC上的高AD=4,tanB=$\frac{3}{4}$,则AC=5.
如图,已知Rt△ABC中,斜边BC上的高AD=4,tanB=$\frac{3}{4}$,则AC=5. 对于上抛物体,在不计空气阻力的情况下,有如下关系式:h=v0t-$\frac{1}{2}$gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
对于上抛物体,在不计空气阻力的情况下,有如下关系式:h=v0t-$\frac{1}{2}$gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.