Question

16．如图，在平面直角坐标系中，抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A（-2，0），C（4，0）两点，和y轴相交于点B，连接AB、BC．
（1）求抛物线的解析式（关系式）；
（2）在直线BC上方的抛物线上，找一点D，使S_△BCD：S_△ABC=1：4，并求出此时点D的坐标．

Answer 1

分析 （1）根据函数图象经过的两点的坐标利用待定系数法确定二次函数的解析式即可；
（2）根据S_△ABC利用S_△BCD：S_△ABC=1：4，求得S_△BCD=$\frac{1}{4}$S_△ABC=3．设D的坐标为（x，-$\frac{1}{2}$x²+x+4），作DE⊥x轴于点E，利用S_△BCD=S_梯形BOED+S_△DCE-S_△BOC即可求得点D的坐标（1，$\frac{9}{2}$）或（3，$\frac{5}{2}$）．

解答 解：（1）∵抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A（-2，0），C（4，0）两点，
∴$\left\{\begin{array}{l}{-\frac{1}{2}×4-2b+c=0}\\{-\frac{1}{2}×16+4b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=1}\\{c=4}\end{array}\right.$，
∴抛物线的表达式为：y=-$\frac{1}{2}$x²+x+4；
（2）由y=-$\frac{1}{2}$x²+x+4可知B（0，4），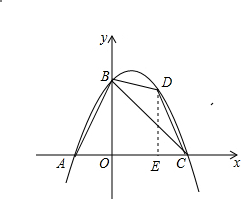
∵A（-2，0），C（4，0），
∴AC=6，OB=4，
∵S_△ABC=$\frac{1}{2}$×6×4=12，S_△BCD：S_△ABC=1：4，
∴S_△BCD=$\frac{1}{4}$S_△ABC=3．
如图所示，设在直线BC上方的抛物线上，找一点D的坐标为（x，-$\frac{1}{2}$x²+x+4），作DE⊥x轴于点E，则
S_△BCD=S_梯形BOED+S_△DCE-S_△BOC
=$\frac{1}{2}$（-$\frac{1}{2}$x²+x+4+4）•x+$\frac{1}{2}$（4-x）（-$\frac{1}{2}$x²+x+4）-$\frac{1}{2}$×4×4=3．
即x²-4x+3=0，
解得x₁=1，x₂=3．
∴点D的坐标为（1，$\frac{9}{2}$）或（3，$\frac{5}{2}$）．

点评 本题考查了待定系数法求二次函数的解析式以及二次函数的综合知识，特别是题目中涉及到的将点的坐标转化为线段的长更是解决二次函数知识的常用方法．