题目内容
10.已知一条抛物线的形状与抛物线y=2x2+3形状相同,与另一条抛物线y=-$\frac{1}{2}$(x+1)2-2的顶点坐标相同,这条抛物线的解析式为y=2(x+1)2-2,y=-2(x+1)2-2.分析 设抛物线的顶点式为y=±2(x-h)2+k,再求得顶点坐标是(-1,-2),代入即可确定解析式.
解答 解:∵一条抛物线的形状与抛物线y=2x2+3形状相同,
∴a=±2,
设抛物线的顶点式为y=±2(x-h)2+k,
由y=-$\frac{1}{2}$(x+1)2-2可知顶点(-1,-2)
∴此抛物线顶点坐标是(-1,-2),
∴抛物线的顶点式为y=±2(x+1)2-2.
故答案为:y=2(x+1)2-2,y=-2(x+1)2-2.
点评 本题考查了用待定系数法求二次函数的解析式以及二次函数的性质,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列各组线段中,能成比例的是( )
| A. | 3,6,7,9 | B. | 2,5,6,8 | C. | 3,6,9,18 | D. | 1,2,3,4 |
15.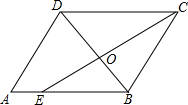 如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
 如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{3}$ |

 如图所示,第n个图形由正n+2边形拓展而来,(n=1,2,…),则第8个图形共有110个顶点.
如图所示,第n个图形由正n+2边形拓展而来,(n=1,2,…),则第8个图形共有110个顶点. 如图,P为⊙O外一点,OP⊥弦AB,PA与⊙O相切于点A,BC∥OP,交⊙O于点C.若OC=2,OP=$\frac{7}{2}$,求弦AB的长.
如图,P为⊙O外一点,OP⊥弦AB,PA与⊙O相切于点A,BC∥OP,交⊙O于点C.若OC=2,OP=$\frac{7}{2}$,求弦AB的长.