Question

15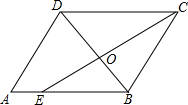．如图所示，在?ABCD中，CE是∠DCB的平分线，且交AB于E，DB与CE相交于O，已知AB=6，BC=4，则$\frac{OB}{DB}$等于（　　）

• A． $\frac{1}{3}$
• B． $\frac{2}{5}$
• C． $\frac{3}{7}$
• D． $\frac{2}{3}$

Answer 1

分析 先利用平行四边形的性质得到CD∥AB=6，再证明∠2=∠3得到BE=BC=4，接着证明△BEO∽△DCO，则利用相似比得到$\frac{OB}{OD}$=$\frac{BE}{CD}$=$\frac{2}{3}$，然后利用比例性质得到$\frac{BO}{BD}$得值．

解答 解：∵四边形ABCD为平行四边形，
∴CD∥AB=6，
∵∠1=∠2，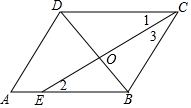
∵CE是∠DCB的平分线，
即∠1=∠3，
∴∠2=∠3，
∴BE=BC=4，
∵BE∥CD，
∴△BEO∽△DCO，
∴$\frac{OB}{OD}$=$\frac{BE}{CD}$=$\frac{4}{6}$=$\frac{2}{3}$，
∴$\frac{BO}{BO+DO}$=$\frac{2}{3+2}$=$\frac{2}{5}$，
即$\frac{BO}{DB}$=$\frac{2}{5}$．
故选B．

点评 本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在运用三角形相似的性质时主要利用相似比计算相应线段的长．