题目内容
6.将抛物线C1:y=-x2-2x,绕着点M(1,0)旋转180°后,所得到的新抛物线C2的解析式是y=(x-3)2-1.分析 先利用配方法得到抛物线C1的顶点坐标为(-1,1),再利用中心对称的性质得到点(-1,1)关于M(1,0)中心对称的点的坐标为(3,-1),由于抛物线C1绕着点M(1,0)旋转180°后抛物线形状不变,只是开口方向相反,且旋转后抛物线的顶点坐标为(3,-1),于是可根据顶点式写出新抛物线解析式.
解答 解:∵y=-x2-2x=-(x+1)2+1,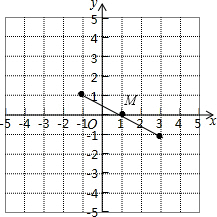
∴抛物线C1的顶点坐标为(-1,1),
∵点(-1,1)关于M(1,0)中心对称的点的坐标为(3,-1),
∴抛物线C1绕着点M(1,0)旋转180°后,所得到的新抛物线C2的解析式为y=(x-3)2-1.
故答案为y=(x-3)2-1.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
1.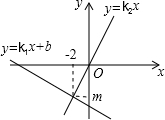 同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
 同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )| A. | x>-2 | B. | x<-2 | C. | x<2 | D. | x<4 |
18.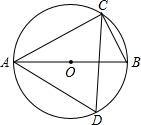 如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
 如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )| A. | 52° | B. | 56° | C. | 62° | D. | 72° |
15.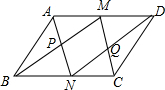 如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
 如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )| A. | AP=PN | B. | NQ=QD | ||
| C. | 四边形PQNM是矩形 | D. | △ABN是等边三角形 |