题目内容
18.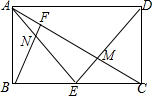 如图,矩形ABCD中,E是BC的中点,ED⊥AE,ED交AC于点M,BF⊥AC于点F,交AE于点N,给出下列结论:①△ABN≌△ECM;②tan∠EAC=$\frac{1}{3}$;③AF:FM:CM=3:7:5,其中正确的是( )
如图,矩形ABCD中,E是BC的中点,ED⊥AE,ED交AC于点M,BF⊥AC于点F,交AE于点N,给出下列结论:①△ABN≌△ECM;②tan∠EAC=$\frac{1}{3}$;③AF:FM:CM=3:7:5,其中正确的是( )| A. | ① | B. | ①② | C. | ②③ | D. | ①②③ |
分析 根据SAS判定△ABE≌△DCE,得出△ADE是等腰直角三角形,再根据ASA即可判定△ABN≌△ECM;根据CE∥AD,即可得到$\frac{EM}{DM}$=$\frac{CE}{AD}$=$\frac{1}{2}$,进而得出EM=$\frac{1}{3}$DE=$\frac{1}{3}$AE,即可得到Rt△AEM中,tan∠EAC=$\frac{EM}{AE}$=$\frac{1}{3}$;根据射影定理即可得到AF=$\frac{\sqrt{5}}{5}$,根据CE∥AD,即可得到CM=$\frac{1}{3}$AC=$\frac{\sqrt{5}}{3}$,再根据FM=$\sqrt{5}$-$\frac{\sqrt{5}}{5}$-$\frac{\sqrt{5}}{3}$=$\frac{7}{15}\sqrt{5}$,即可得出AF:FM:CM=3:7:5.
解答  解:E是BC的中点,
解:E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠ABE=∠DCE}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE(SAS),
∴AE=DE,而AE⊥DE,
∴△ADE是等腰直角三角形,
∴∠EAD=∠EDA=45°,
∴∠BAE=∠BEA=∠CDE=∠CED=45°,
∴AB=BE=CE=CD,
∵ED⊥AE,∠ABE=90°,
∴∠BAN+∠AEB=90°,∠CEM+∠AEB=90°,
∴∠BAN=∠CEM,
∵Rt△ABC中,BF⊥AC,
∴∠ABN+∠BAC=90°,∠ECM+∠BAC=90°,
∴∠ABN=∠ECM,
在△ABN和△ECM中,
$\left\{\begin{array}{l}{∠BAN=∠CEM}\\{AB=EC}\\{∠ABN=∠ECM}\end{array}\right.$,
∴△ABN≌△ECM(ASA),故①正确;
∵CE∥AD,
∴$\frac{EM}{DM}$=$\frac{CE}{AD}$=$\frac{1}{2}$,
∴EM=$\frac{1}{3}$DE=$\frac{1}{3}$AE,
∴Rt△AEM中,tan∠EAC=$\frac{EM}{AE}$=$\frac{1}{3}$,故②正确;
设AB=BE=CE=CD=1,则Rt△ABC中,AC=$\sqrt{5}$,
∵BF⊥AC,
∴AB2=AF×AC,即1=AF×$\sqrt{5}$,
∴AF=$\frac{\sqrt{5}}{5}$,
∵CE∥AD,
∴$\frac{CM}{AM}$=$\frac{CE}{AD}$=$\frac{1}{2}$,
∴CM=$\frac{1}{3}$AC=$\frac{\sqrt{5}}{3}$,
∴FM=$\sqrt{5}$-$\frac{\sqrt{5}}{5}$-$\frac{\sqrt{5}}{3}$=$\frac{7}{15}\sqrt{5}$,
∴AF:FM:CM=3:7:5,故③正确,
故选:D.
点评 本题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的性质,解直角三角形,平行线分线段成比例定理以及射影定理的综合应用,解题时注意:每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

 名校课堂系列答案
名校课堂系列答案| A. | -a6 | B. | -a5 | C. | a6 | D. | a5 |
 已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.
已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.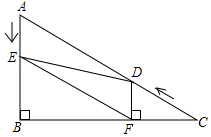 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.