题目内容
9. 如图,△DEF的边长分别为1,$\sqrt{3}$,2,正六边形网格是由24个边长为2的正三角形组成,选择格点为顶点画△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.
如图,△DEF的边长分别为1,$\sqrt{3}$,2,正六边形网格是由24个边长为2的正三角形组成,选择格点为顶点画△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.
分析 根据题意可得:在正六边形网格找与△DEF相似的三角形;即找三边的比值为1:$\sqrt{3}$:2的直角三角形;分析图形可得:共三种情况得出答案即可.
解答  解:∵△DEF的边长分别为1,$\sqrt{3}$,2
解:∵△DEF的边长分别为1,$\sqrt{3}$,2
∴△DEF为直角三角形,∠F=30°,∠D=60°,
根据等边三角形的三线合一,可作三边比为1:($\sqrt{3}$+$\sqrt{3}$):2的三角形,
故相似比$\frac{AB}{DE}$=k,k可取2,2$\sqrt{3}$,4.
故答案为:2,2$\sqrt{3}$,4.
点评 此题主要考查了相似三角形的判定与性质,结合各边长得出符合题意的图形是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,直线AB∥CD,BC平分∠ABD,∠1=75°,求∠2的度数.
如图,直线AB∥CD,BC平分∠ABD,∠1=75°,求∠2的度数. 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有4.
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有4. 若a、b、c在数轴上的位置如图,则|a|-|b-c|+|c|=b-a.
若a、b、c在数轴上的位置如图,则|a|-|b-c|+|c|=b-a. 如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$.
如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$.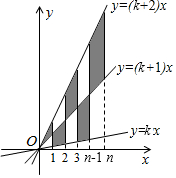 在x正半轴上有n个连续整数点,它们的横坐标依次为1,2,3,…,n,分别过这些点作x轴的垂线与三条直线y=kx,y=(k+1)x,y=(k+2)x相交,其中k>0,则图中阴影部分的面积总和是$\frac{1}{2}$n2.
在x正半轴上有n个连续整数点,它们的横坐标依次为1,2,3,…,n,分别过这些点作x轴的垂线与三条直线y=kx,y=(k+1)x,y=(k+2)x相交,其中k>0,则图中阴影部分的面积总和是$\frac{1}{2}$n2.