顺次连接三角形三边的中点.所得的三角形与原三角形对应高的比是( )A．1:4B．1:3C．1:$\sqrt{2}$D．1:2 题目和参考答案——青夏教育精英家教网—

题目内容

13．顺次连接三角形三边的中点，所得的三角形与原三角形对应高的比是（　　）

A．

1：4

B．

1：3

C．

1：$\sqrt{2}$

D．

1：2

分析根据“相似三角形的对应高的比等于相似比”求解即可．

解答解：因为顺次连接三角形三边的中点，所得的三角形与原三角形相似，
且：相似三角形对应高的比等于相似比．
又因为：顺次连接三角形三边的中点，所得的三角形的三边的长等于原三角形对应边的一半，
所以：顺次连接三角形三边的中点，所得的三角形与原三角形对应高的比是 1：2
故：选D

点评本题考查了相似三角形的性质、三角形中位线定理，解题的关键是掌握并理解该知识要点．

练习册系列答案

相关题目

3．如果等腰三角形的一个内角为50度，那么这个等腰三角形的底角是50或65度．

4．某品牌商品，按标价八折出售，仍可获得10%的利润，若该商品标价275元，则商品的进价为200元．

1．已知△ABC中，∠A=20°，∠B=70°，那么三角形△ABC是（　　）

8．

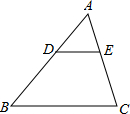如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=6，S_△ADE：S_△ABC=9：49，则EC的长是（　　）

18．

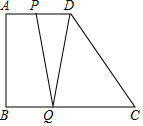已知：在梯形ABCD中，AD∥BC，∠ABC=90°，AD=12，BC=24，动点P沿AD方向从点A出发到D点以每秒1个单位的速度运动，动点Q从点C出发，沿CB方向以每秒2个单位的速度运动，P、Q同时出发，当点P停止运动时，点Q也随之停止运动，连接PQ、DQ，设点P运动的时间为x秒，请求出当x为何值时，△PDQ≌△CQD．

5．已知方程组$\left\{\begin{array}{l}{x+y=1-a}\\{x-y=3a+5}\end{array}\right.$ 的解x为正数，y为非负数．
（1）求a的取值范围．
（2）化简|a+3|+|a-1|

2．把$\frac{1}{ab}$和$\frac{2a-b}{{a}^{2}}$化成分母相同的分式．
$\frac{1}{ab}$=$\frac{a}{{a}^{2}b}$
$\frac{2a-b}{{a}^{2}}$=$\frac{2ab{-b}^{2}}{{a}^{2}b}$．

3．下列函数中，y的值随x的增大而减小的是（　　）

试题分类