Question

18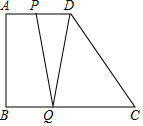．已知：在梯形ABCD中，AD∥BC，∠ABC=90°，AD=12，BC=24，动点P沿AD方向从点A出发到D点以每秒1个单位的速度运动，动点Q从点C出发，沿CB方向以每秒2个单位的速度运动，P、Q同时出发，当点P停止运动时，点Q也随之停止运动，连接PQ、DQ，设点P运动的时间为x秒，请求出当x为何值时，△PDQ≌△CQD．

Answer 1

分析 根据题意表示出AP、PD、CQ的长，利用全等三角形的性质，对应边相等得：PD=CQ，列方程解出即可．

解答 解：由题意得：AP=x，CQ=2x，则PD=12-x，
∵△PDQ≌△CQD，
∴PD=CQ，
即12-x=2x，
x=4，
答：当x为4秒时，△PDQ≌△CQD．

点评 本题动点运动问题，主要考查了三角形全等的性质，难度不大，此类题的解题思路为：①先根据动点运动的时间和速度表示相关线段的长，②根据已知列方程或等量关系式求解．