题目内容
5．
如图，AD是正五边形ABCDE的一条对角线，则∠BAD=72°．
分析 利用多边形内角和公式求得∠E的度数，在等腰三角形AED中可求得∠EAD的读数，进而求得∠BAD的度数．
解答 解：∵正五边形ABCDE的内角和为（5-2）×180°=540°，
∴∠E=$\frac{1}{5}$×540°=108°，∠BAE=108°
又∵EA=ED，
∴∠EAD=$\frac{1}{2}$×（180°-108°）=36°，
∴∠BAD=∠BAE-∠EAD=72°，
故答案为：72°．
点评 本题考查了正多边形的计算，重点掌握正多边形内角和公式是关键．
练习册系列答案
相关题目
10．下列计算正确的是（ ）
| A． | （-3a2b）3=-3a5b3 | B． | $\frac{1}{2}$ab2•（-4a3b）=-2a4b3 | ||
| C． | 4m3n2÷m3n2=0 | D． | a5-a2=a3 |
17．
如图，将一个边长分别为4、8的矩形纸片ABCD折叠，使点C与点A重合（AB=4，BC=8），则折痕EF的长度为（ ）
如图，将一个边长分别为4、8的矩形纸片ABCD折叠，使点C与点A重合（AB=4，BC=8），则折痕EF的长度为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{5}$ | D． | 2$\sqrt{5}$ |
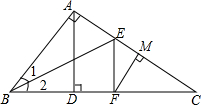如图，△ABC中，∠BAC=90°，AD⊥BC，BE平分∠ABC，EF⊥BC，FM⊥AC，垂足分别是D，F，M，求证：FM=FD．