题目内容
10．如果直角三角形的三条边分别为4、5、a，那么a2的值等于9或41．分析 此题有两种情况，一是当这个直角三角形的斜边的长为5时；二是当这个直角三角形两条直角边的长分别为4和5时，由勾股定理分别求出此时的a2值即可．
解答 解：当这个直角三角形的斜边的长为5时，
a2=52-42=9；
当这个直角三角形两条直角边的长分别为4和5时，
a2=52+42=41．
故a的值为9或41．
故答案为：9或41．
点评 本题考查勾股定理的知识，解答此题的关键是直角三角形的斜边没有确定，所以要进行分类讨论，注意不要漏解，难度一般．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
18．
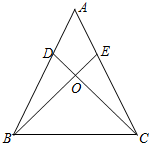如图，在△ABC中，已知点D、E分别在AB、AC上，BE与CD相交于点O，依据下列各个选项中所列举的条件，不能说明AB=AC的是（ ）
如图，在△ABC中，已知点D、E分别在AB、AC上，BE与CD相交于点O，依据下列各个选项中所列举的条件，不能说明AB=AC的是（ ）| A． | BE=CD，∠EBC=∠DCB | B． | AD=AE，BE=CD | C． | OD=OE，∠ABE=∠ACD | D． | BE=CD，BD=CE |
5．若$\frac{m}{n}$=0，那么一定有（ ）
| A． | n=0 | B． | m=0且n≠0 | C． | m=n=0 | D． | m=0或n=0 |