题目内容
13.例:已知整式A=a3+3a2b+2b2+5b-2,整式B=a3-a2b+b2-5b-3,试比较A与B的大小.解析:比较A与B的大小,可以转化为作两者的差,由差的正负来决定大小.
A-B=(a3+3a2+2b2+5b-2)-(a3-a2+b2-5b-3)
=a3+3a2+2b2+5b-2-a3+a2-b2+5b+3=4a2+b2+1
∵a2,b2是非负数,∴4a2+b2也是非负数,∴4a2+b2+1>0
∴A-B>0,∴A>B.
仿照上述思想:试比较多项式A=4x2-3x-5y2-6与多项式B=5x2-3x+2y2+4的大小.
分析 根据材料,求A-B,若差>0,A>B;若差<0,A<B.
解答 解:A-B=(4x2-3x-5y2-6)-(5x2-3x+2y2+4)
=-5x2-7y2-10,
∵x2,y2是非负数,
∴-5x2-7y2是非正数,
∴-5x2-7y2-10<0
∴A-B<0,
∴A<B.
点评 本题考查了整式的加减,掌握合并同类项得法则以及作差法比较两个数或整式的大小是解题的关键.

练习册系列答案
相关题目
18.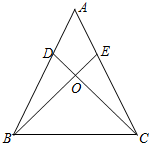 如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
 如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )| A. | BE=CD,∠EBC=∠DCB | B. | AD=AE,BE=CD | C. | OD=OE,∠ABE=∠ACD | D. | BE=CD,BD=CE |
5.若$\frac{m}{n}$=0,那么一定有( )
| A. | n=0 | B. | m=0且n≠0 | C. | m=n=0 | D. | m=0或n=0 |