题目内容
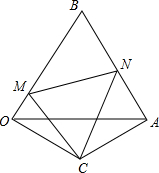 如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是考点:旋转的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:由旋转可知CM=CN,结合条件可证明△OMC≌△ANC,可证明△AMN为等边三角形,且可求得OM的长,可求得答案.
解答:解:∵OC=AC,∠OCA=120°,
∴∠COA=∠CAO=30°,
又∵△BOA为等边三角形,
∴∠BOA=∠BAO=60°,
∴∠MOC=∠NAC=90°,
在Rt△OCM和Rt△ACN中,
,
∴△OCM≌△ACN(HL),
∴OM=AN,∠MCO=NCA=30°,
∴BM=BN,
∴△AMN为等边三角形,
在△OAC中,OA=2,可求得OC=
,
在Rt△MOC中可求得OM=
,
∴BM=BO-OM=2-
=
,
∴△BMN的周长为4.
故答案为:4.
∴∠COA=∠CAO=30°,
又∵△BOA为等边三角形,
∴∠BOA=∠BAO=60°,
∴∠MOC=∠NAC=90°,
在Rt△OCM和Rt△ACN中,
|
∴△OCM≌△ACN(HL),
∴OM=AN,∠MCO=NCA=30°,
∴BM=BN,
∴△AMN为等边三角形,
在△OAC中,OA=2,可求得OC=
2
| ||
| 3 |
在Rt△MOC中可求得OM=
| 2 |
| 3 |
∴BM=BO-OM=2-
| 2 |
| 3 |
| 4 |
| 3 |
∴△BMN的周长为4.
故答案为:4.
点评:本题主要考查旋转的性质及等边三角形的判定和性质,利用旋转的性质判断出△BMN为等边三角形是解题的关键,注意勾股定理的应用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列是一元一次方程的是( )
| A、x2-4=0 | ||
| B、x+y=3 | ||
C、
| ||
| D、5x=1 |
 已知:如图AB∥DE,AC∥DF,BE=CF,此时AB与DE有什么关系?试说明理由.
已知:如图AB∥DE,AC∥DF,BE=CF,此时AB与DE有什么关系?试说明理由.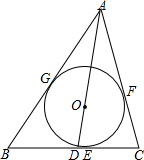 如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r.
如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r. 如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为
如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=
在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD= 如图所示,AD是△ABC的角平分线,CE∥AD交BA的延长线于点E,求证:
如图所示,AD是△ABC的角平分线,CE∥AD交BA的延长线于点E,求证: