题目内容
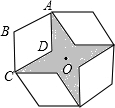 如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )
如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )| A、8 | ||
B、12-4
| ||
C、1+
| ||
D、12-2
|
考点:旋转的性质
专题:
分析:连接OA、OC和AC,由旋转性质可知△AOC为等腰直角三角形,△ACD为菱形的一半,可求得△AOC中阴影部分的面积,由对称性可求得阴影部分的面积.
解答: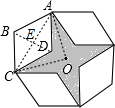 解:如图,连接AO、CO,连接AC和BD,交于点E
解:如图,连接AO、CO,连接AC和BD,交于点E
由旋转可知OA=CO,∠AOC=90°,
∵∠BAD=60°,AB=2,
∴BD=AB=2,AE=
,
∴AC=2
,AO=
,
∴S阴影=4(S△AOC-S△ADC)
=4(S△AOC-
S菱形ABCD)
=4(
AO•CO-
×
AC•BD)
=4(
×
×
-
×2×2
)
=12-4
.
故选B.
 解:如图,连接AO、CO,连接AC和BD,交于点E
解:如图,连接AO、CO,连接AC和BD,交于点E由旋转可知OA=CO,∠AOC=90°,
∵∠BAD=60°,AB=2,
∴BD=AB=2,AE=
| 3 |
∴AC=2
| 3 |
| 6 |
∴S阴影=4(S△AOC-S△ADC)
=4(S△AOC-
| 1 |
| 2 |
=4(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4(
| 1 |
| 2 |
| 6 |
| 6 |
| 1 |
| 4 |
| 3 |
=12-4
| 3 |
故选B.
点评:本题主要考查旋转和菱形的性质,掌握菱形的性质及旋转的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题是真命题的是( )
| A、4是2的平方根 |
| B、2是4的算术平方根 |
| C、0的算术平方根不存在 |
| D、-1是-1的算术平方根 |
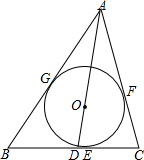 如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r.
如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r.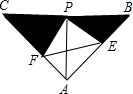 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF= 在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=
在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=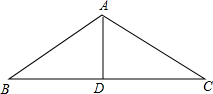 如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.
如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.