题目内容
8.设反比例函数y=$\frac{2}{x}$与一次函数y=x+3的图象的一个交点坐标为(m,n),则$\frac{1}{m}-\frac{1}{n}$的值为$\frac{3}{2}$.分析 根据题意得到mn=2,n-m=3,代入原式计算即可.
解答 解:∵反比例函数y=$\frac{2}{x}$与一次函数y=x+3的图象的一个交点坐标为(m,n),
∴n=$\frac{2}{m}$,n=m+3,
∴mn=2,n-m=3,
∴$\frac{1}{m}-\frac{1}{n}$=$\frac{n-m}{mn}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握反比例函数与一次函数图象上点的坐标特征是解题的关键.

练习册系列答案
相关题目
7. 如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
 如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
8.某人沿倾斜角为30°的斜坡前进6米,则他上升的最大高度为( )
| A. | 3米 | B. | 3$\sqrt{3}$米 | C. | $\sqrt{3}$米 | D. | 2$\sqrt{3}$米 |
18. 如图所示,P是反比例函数y=的图象上一点,过点P分别向x轴和y轴引垂线,若S阴影=3,则k的值是( )
如图所示,P是反比例函数y=的图象上一点,过点P分别向x轴和y轴引垂线,若S阴影=3,则k的值是( )
 如图所示,P是反比例函数y=的图象上一点,过点P分别向x轴和y轴引垂线,若S阴影=3,则k的值是( )
如图所示,P是反比例函数y=的图象上一点,过点P分别向x轴和y轴引垂线,若S阴影=3,则k的值是( )| A. | 3 | B. | -3 | C. | ±3 | D. | -9 |
 如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )
如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )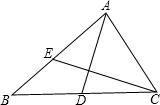 如图,D、E分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,设BC=a,AC=b,AB=c,给出以下几个结论:
如图,D、E分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,设BC=a,AC=b,AB=c,给出以下几个结论: