题目内容
20.如图所示,图(1)中含“○”的矩形有1个,图(2)中含“○”的矩形有7个,图(3)中含“○”的矩形有17个,按此规律,图(6)中含“○”的矩形有( )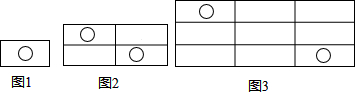
| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
分析 ①先计算每个图形中单个矩形的个数:图(1):12=1,图2:22=4,则图(6):62=36;
②由1个矩形中含“○”有2个,由2个矩形中含“○”有:2+2=4个(发现与2的因数有关系),由3个矩形中含“○”有:2+2=4个,…,由36个矩形中含“○”有1个,最后相加为71个.
解答 解:图(6)中,62=36, 1个矩形:1×2=2个,
1个矩形:1×2=2个,
2个矩形:1×2:2个,
2×1:2个,
3个矩形:1×3:2个
3×1:2个
4个矩形:1×4:2个
4×1:2个
2×2:2个
5个矩形:1×5:2个
5×1:2个
6个矩形:1×6:2个
6×1:2个
2×3:2个
3×2:2个
8个矩形:2×4:2个
4×2:2个
9个矩形:3×3:2个
10个矩形:2×5:2个
5×2:2个
12个矩形:2×6:2个
6×2:2个
3×4:2个
4×3:2个
15个矩形:3×5:2个
5×3:2个
16个矩形:4×4:2个
18个矩形;3×6:2个
6×3:2个
20个矩形:4×5:2个
5×4:2个
24个矩形:4×6:2个
6×4:2个
25个矩形:5×5:2个
30个矩形:5×6:2个
6×5:2个
36个矩形:6×6:1个,
总计和为71个;
故选B.
点评 这是一个图形变化类的规律题,这类题属于常考题型,但分值都不高;做好此类题要从第一个图形入手,分析第一个图形结论的得出,此题不是完全数字的变化,还有图形的变化,相结合才能得出结论,最后发现与矩形个数的因数有关,依次计算即可.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | -2是4的平方根 | B. | 4的平方根是2 | C. | 2没有平方根 | D. | $\root{3}{3}$大于$\frac{3}{2}$ |
20.为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
| A. | 9800名学生是总体 | B. | 每个学生是个体 | ||
| C. | 100名学生是所抽取的一个样本 | D. | 样本容量是100 |
15.在线段、等边三角形、等腰梯形、矩形、平行四边形、菱形、正方形、圆这些图形中,既是中心对称图形又是轴对称图形的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
5.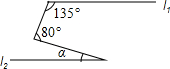 如图直线l1∥l2,则∠α的大小( )
如图直线l1∥l2,则∠α的大小( )
 如图直线l1∥l2,则∠α的大小( )
如图直线l1∥l2,则∠α的大小( )| A. | 35° | B. | 45° | C. | 55° | D. | 80° |
12.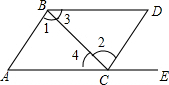 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |
9.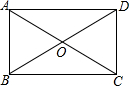 如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )
如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )
 如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )
如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )| A. | 5 | B. | $2\sqrt{5}$ | C. | $2\sqrt{13}$ | D. | $\sqrt{13}$ |
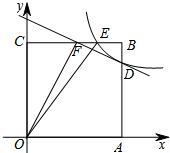 如图,正方形OABC的边长为4,反比例函数y=$\frac{k}{x}$(k>0)的图象与线段AB交于点D,与线段BC交于点E,点E的坐标为(3,4).
如图,正方形OABC的边长为4,反比例函数y=$\frac{k}{x}$(k>0)的图象与线段AB交于点D,与线段BC交于点E,点E的坐标为(3,4).