题目内容
 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连结AA′,若∠1=25°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连结AA′,若∠1=25°,则∠B的度数是( )| A、70° | B、65° |
| C、60° | D、55° |
考点:旋转的性质
专题:
分析:根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.
解答:解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=25°+45°=70°,
由旋转的性质得∠B=∠A′B′C=70°.
故选:A.
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=25°+45°=70°,
由旋转的性质得∠B=∠A′B′C=70°.
故选:A.
点评:本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
 如图可以拼成的几何体是( )
如图可以拼成的几何体是( )| A、三梭柱 | B、四棱柱 |
| C、圆柱 | D、圆锥 |
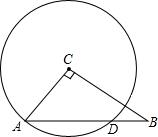 如图,Rt△ABC中,∠C=90°,⊙C经过点A,交AB于点D.
如图,Rt△ABC中,∠C=90°,⊙C经过点A,交AB于点D. 如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数. 如图,△ABC是等腰三角形,∠BAC=36°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
如图,△ABC是等腰三角形,∠BAC=36°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,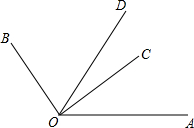 如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数. 已知有理数a、b、c在数轴上的位置如图所示,化简:|a|-|-a+b|+|c-a|+|b-c|.
已知有理数a、b、c在数轴上的位置如图所示,化简:|a|-|-a+b|+|c-a|+|b-c|. 若AB∥CD,∠B、∠E、∠E、∠D三者满足关系
若AB∥CD,∠B、∠E、∠E、∠D三者满足关系