题目内容
20.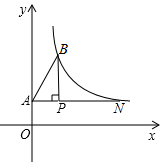 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.(1)求k的值;
(2)求直线AB的解析式.
分析 (1)由点P的坐标可得出A点的坐标以及线段AP的长度,通过解直角三角形可求出BP的长度,结合点P的坐标即可得出B点的坐标,再利用待定系数法即可求出反比例函数的解析式;
(2)设直线AB的解析式y=ax+b.结合A、B点的坐标利用待定系数法即可求出直线AB的解析式.
解答 解:(1)∵点P的坐标为(2,$\frac{3}{2}$),
∴AP=2,点A的坐标为(0,$\frac{3}{2}$).
在Rt△ABP中,∠APB=90°,tan∠BAP=$\frac{3}{2}$,AP=2,
∴BP=AP•tan∠BAP=2×$\frac{3}{2}$=3,
∴点B的坐标为(2,$\frac{9}{2}$).
∵点B(2,$\frac{9}{2}$)在反比例函数y=$\frac{k}{x}$(x>0)图象上,
∴$\frac{9}{2}$=$\frac{k}{2}$,解得:k=9.
(2)设直线AB的解析式y=ax+b,
则有$\left\{\begin{array}{l}{\frac{3}{2}=b}\\{\frac{9}{2}=2a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=\frac{3}{2}}\end{array}\right.$.
∴直线AB的解析式为y=$\frac{3}{2}$x+$\frac{3}{2}$.
点评 本题考查了一次函数与反比例函数交点问题、待定系数法求函数解析式以及解直角三角形,解题的关键是:(1)求出点B坐标;(2)利用待定系数法求函数解析式.本题属于基础题,难度不大,解决该题型题目时,通过边角关系找出点的坐标,再利用待定系数法求出函数解析式是关键.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15.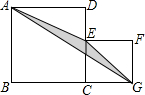 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )| A. | a2-b2 | B. | $\frac{2}{3}({a}^{2}-{b}^{2})$ | C. | $\frac{1}{2}{b}^{2}$ | D. | $\frac{1}{2}{a}^{2}$ |
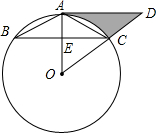 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D. 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°,若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转20度.
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°,若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转20度.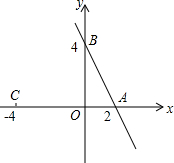 如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).
如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).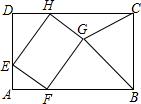 如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.
如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.