题目内容
9.某酒厂生产A、B两种品牌的酒,每天两种酒共生产600瓶,每种酒每瓶的成本和利润如下表所示.设每天共获利y元,每天生产A种品牌的酒x瓶.| A | B | |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
(2)如果该厂每天至少投入成本25000元,且生产B种品牌的酒不少于全天产量的55%,那么共有几种生产方案?并求出每天至少获利多少元?
分析 (1)根据获利y=A种品牌的酒的获利+B种品牌的酒的获利,即可解答.
(2)根据生产B种品牌的酒不少于全天产量的55%,A种品牌的酒的成本+B种品牌的酒的成本≥25000,列出方程组,求出x的取值范围,根据x为正整数,即可得到生产方案;再根据一次函数的性质,即可求出每天至少获利多少元.
解答 解:(1)由题意,每天生产A种品牌的酒x瓶,则每天生产B种品牌的酒(600-x)瓶,
∴y=20x+15(600-x)=9000+5x.
(2)根据题意得:$\left\{\begin{array}{l}{600-x≥600×55%}\\{50x+35(600-x)≥25000}\end{array}\right.$,
解得:266$\frac{2}{3}$≤x≤270,
∵x为整数,
∴x=267、268、269、270,
该酒厂共有4种生产方案:
①生产A种品牌的酒267瓶,B种品牌的酒333瓶;
②生产A种品牌的酒268瓶,B种品牌的酒332瓶;
③生产A种品牌的酒269瓶,B种品牌的酒331瓶;
④生产A种品牌的酒270瓶,B种品牌的酒330瓶;
∵每天获利y=9000+5x,y是关于x的一次函数,且随x的增大而增大,
∴当x=267时,y有最小值,y最小=9000+5×267=10335元.
点评 本题考查了一次函数的应用,关键从表格种获得成本价和利润,然后根据利润这个等量关系列解析式,根据第二问中的利润和成本做为不等量关系列不等式组分别求出解,然后根据一次函数的性质求出哪种方案获利最小.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (x+y2)2=x2+y4 | B. | b6÷b2=b3 | C. | -a2+2a2=a2 | D. | (2y)2×(-y)=-2y3 |
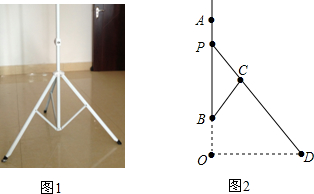
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )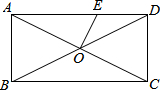 如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5.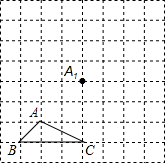 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).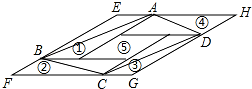 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.