题目内容
1.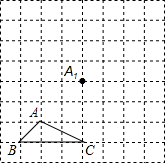 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
分析 (1)按A到A1的平移方向和平移距离,即可得到B和C对应点,从而得到平移后的图形;
(2)把B1和C1绕点A1旋转90°,得到对应点即可得到对应图形;
(3)利用勾股定理和弧长公式即可求解.
解答 解:(1)△A1B1C1就是所求的图形;
(2)△A1B2C2就是所求的图形;
(3)B到B1的路径长是:$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
B1到B2的路径长是:$\frac{90π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
则路径总长是:2$\sqrt{2}$+$\frac{\sqrt{2}}{2}$π.
点评 本题考查了图形的平移和旋转,以及弧长公式,理解图象的旋转过程中每个点经过的路径是弧是关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
11.下列运算正确的是( )
| A. | a3+a4=a7 | B. | a8÷a2=a4 | C. | (2a4)3=8a7 | D. | 2a3•a4=2a7 |
9.某酒厂生产A、B两种品牌的酒,每天两种酒共生产600瓶,每种酒每瓶的成本和利润如下表所示.设每天共获利y元,每天生产A种品牌的酒x瓶.
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且生产B种品牌的酒不少于全天产量的55%,那么共有几种生产方案?并求出每天至少获利多少元?
| A | B | |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
(2)如果该厂每天至少投入成本25000元,且生产B种品牌的酒不少于全天产量的55%,那么共有几种生产方案?并求出每天至少获利多少元?
 已知:如图,在△ABC中,AB=AC,BE、CD是中线.求证:BE=CD.
已知:如图,在△ABC中,AB=AC,BE、CD是中线.求证:BE=CD.