题目内容
七年级学生小明是一个喜欢思考问题而又乐于助人的好学生,一天邻居家读小学的小李,请他帮忙检查作业:
7×9=63; 8×8=64;
8×10=80; 9×9=81;
9×11=99; 10×10=100;
10×12=120; 11×11=121;
11×13=143; 12×12=144;
…,
24×26=624; 25×25=625;
…
小明仔细检查后,夸小李聪明,作业全对了!小明还从这几题中发现了一个规律,请你用含有字母n的等式表示小明发现的这一规律为: .
7×9=63; 8×8=64;
8×10=80; 9×9=81;
9×11=99; 10×10=100;
10×12=120; 11×11=121;
11×13=143; 12×12=144;
…,
24×26=624; 25×25=625;
…
小明仔细检查后,夸小李聪明,作业全对了!小明还从这几题中发现了一个规律,请你用含有字母n的等式表示小明发现的这一规律为:
考点:规律型:数字的变化类
专题:
分析:由提议可知,左边的一列式子:等号的左边的两个因数都相差2;结果比靠右边式子的结果少1.右边的一列式子:等号的左边的两个因数相同,为前面那个式子两个因数中间的那个数.
解答:解:小明发现的这一规律为:(n-1)×(n+1)=n2-1.
故答案为:(n-1)×(n+1)=n2-1.
故答案为:(n-1)×(n+1)=n2-1.
点评:此题考查数字的变化规律,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算6x3÷2x2的结果是( )
| A、2x2 |
| B、3x2 |
| C、3x |
| D、3 |

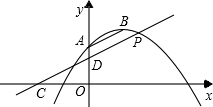 已知抛物线y=ax2-4ax+c经过点A(0,2),顶点B的纵坐标为3.将直线AB向下平移,与x轴、y轴分别交于点C、D,与抛物线的一个交点为P,若D是线段CP的中点,则点P的坐标为
已知抛物线y=ax2-4ax+c经过点A(0,2),顶点B的纵坐标为3.将直线AB向下平移,与x轴、y轴分别交于点C、D,与抛物线的一个交点为P,若D是线段CP的中点,则点P的坐标为 如图,在△ABC中,∠C=90°,AB=10,AC=6,角平分线AE与BF相交于点O,则点O到斜边AB的距离为
如图,在△ABC中,∠C=90°,AB=10,AC=6,角平分线AE与BF相交于点O,则点O到斜边AB的距离为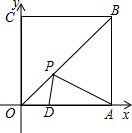 如图,已知四边形OABC为正方形,边长为6,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是
如图,已知四边形OABC为正方形,边长为6,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是