题目内容

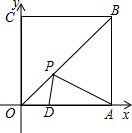如图，已知四边形OABC为正方形，边长为6，点A、C分别在x轴、y轴的正半轴上，点D在OA上，且点D的坐标为（2，0），点P是OB上的一个动点，则PD+PA的最小值是
 
．
考点：轴对称-最短路线问题,坐标与图形性质,正方形的性质
专题：
分析：作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长，利用勾股定理即可求解．
解答：解：作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长．
则OD′=2，
因而AD′=
OD′2+OA2
=
40
=2
10
．
则PD+PA和的最小值是2
10
．
故答案是：2
10
．
点评：本题考查了正方形的性质，以及最短路线问题，正确作出P的位置是关键．
练习册系列答案
相关题目
如图1，矩形纸片ABCD中，AB=2
3
，BC=6，将矩形沿对角线AC剪开，解答以下问题：
（1）将△ACD绕点C顺时针旋转60°，△A1CD1是旋转后的新位置（图2），
①试判断△ACA1的形状，并说明理由．
②求A，A1的距离；
（2）将△ACD沿对角线AC向下翻折（点A、点C位置不动，△ACD和△ABC落在同一平面内），△ACD2是翻折后的新位置（图3），AD2交BC于E，求AE的长．
七年级学生小明是一个喜欢思考问题而又乐于助人的好学生，一天邻居家读小学的小李，请他帮忙检查作业：
7×9=63；     8×8=64；
8×10=80；    9×9=81；
9×11=99；    10×10=100；
10×12=120；  11×11=121；
11×13=143；  12×12=144；
…，
24×26=624；  25×25=625；
…
小明仔细检查后，夸小李聪明，作业全对了！小明还从这几题中发现了一个规律，请你用含有字母n的等式表示小明发现的这一规律为：
 
．
如图，将△ABC纸片折叠，使点A落在边BC上，记落点为点D，且折痕EF∥BC，若BC=4，则EF的长度为
 
．
如图，AB∥CD，CE平分∠BCD，∠DCE=16°，则∠B等于
 
．
如图，△ABC中，∠A=40°，点E，F在AB，AC上，沿EF向内折叠△AEF，得△DEF，则图中∠1+∠2等于
 
．
将直线y=2x+1向下平移4个单位得到直线l，则直线l的解析式为
 
．
一个长方形的长减少5厘米，宽增加2厘米，就成为一个正方形，并且正方形的面积等于原来长方形的面积，则原来长方形的长和宽各是多少？如果设原来长方形的长是xcm，宽是ycm，下面所列出的四个方程组中，正确的是（　　）
A、
2x-5y=10
x-y=7
B、
2x-5y=10
x+y=7
C、
2x+5y=10
x-y=7
D、
2x+5y=10
x+y=7
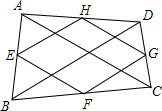如图，四边形ABCD．已知AC=BD，E、F、G，H分别是边AB、BC、CD、DA的中点，连接EF、FG、GH、HE，四边形EFGH一定是（　　）
A、正方形B、矩形
C、菱形D、平行四边形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网